1. Cierto día Sebastián escucha, en una conversación sobre empleo digno en Colombia, que una persona que trabaja como ayudante de volqueta se puede ganar mensualmente las tres cuartas partes del Salario Mínimo Legal Vigente (SMLV). Un SMLV está en $535.600, significa que el ayudante de bus se gana
2. Un tanque está lleno hasta su capacidad, con 350 litros de agua. Se abre una llave que deja salir 100 litros de agua por 20 minutos. El tiempo necesario, en minutos, para vaciar el tanque en estas condiciones es de
3. Sebastián corre a una rapidez de 3 metros cada segundo (se escribe 3m/s). Cierto día sale de su casa al colegio corriendo y se tardó 25 minutos (300 segundos). La distancia, en metros, que separa al colegio de la casa de Sebastián es de
4. Estefanía invierte $100.000 en un negocio, durante un año. Cada mes se gana la quinta parte de lo que invirtió y lo reinvierte, aumentando el capital. Por ejemplo, en enero se ganó $20.000, los reinvierte y el nuevo capital para febrero es de $120.000. En estas condiciones, la cantidad de dinero que se gana en junio es de
Responde los problemas 5, 6 y 7 de acuerdo con la siguiente información.
Se forman fichas didácticas triangulares, rectangulares y circulares de colores amarillo, azul, blanco y verde, fabricadas en madera, plástico o metal.
5. La cantidad de fichas que se pueden formar es de
6. Se escogen 50 niños para extraer algunas fichas de un cajón, al azar. Se registran las fichas que sacan en la siguiente tabla.
Al realizar una tabla de frecuencia por color, se puede afirmar que
7. Al realizar una tabla de frecuencia por Material de la ficha, se puede concluir que
8. La figura que se muestra es un triángulo equilátero al cual se la han dibujado otros triángulos equiláteros desde la mitad de sus lados. El área del triángulo grande es de 120 cm cuadrados, calcular el área de la fugura que se encuentra sombreada.
9. Sebastián compra un artículo en un valor Vi y lo vende en un valor Vf. Cierto día compra k artículos para venderlos, pero cuenta con la mala suerte de habérsele perdido m artículos. El valor total de la ganancia de Sebastián se calcula mediante la fórmula:
10. En una granja hay 10 gallinas y 25 patos. Las gallinas se comen G gramos de maíz diario mientras que los patos se comen P gramos de maíz en el mismo tiempo. ¿Qué cantidad de maíz, en gramos, come más un pato que una gallina, en estas condiciones?
11. En un triángulo recto, se cumple que Sen(a) = 13/5. El valor de la razón trigonométrica Cos(a) es
12. Un vehículo consume un cuarto de galón de gasolina cuando recorre 60 kilómetros. Significa que la variación del número de galones G con relación a la distancia recorrida X en Kilómetros, es de
13. Lee con atención el siguiente cuento.
“Henry miró el reloj. Dos de la madrugada. Cerró el blog de semilleros con desesperación. Seguro que mañana sería reprobado. Entre más quería hundirse en la geometría, menos la entendía. Dos fracasos ya, y sin duda iba a perder un año. Sólo un milagro podría salvarlo. Se levantó. ¿Un milagro? ¿Y por qué no? Siempre se había interesado en la magia. Tenía libros. Había encontrado instrucciones sencillísimas para llamar a los genios de la antigüedad a su voluntad. Nunca había hecho la prueba. Era el momento, ahora o nunca.
Sacó del estante el mejor libro para invocar. Era fácil. Algunas fórmulas. Dibujar en un plano un rombo de cuyas diagonales midan 10 y 24 dm y poner el libro en él y pedir lo que desea que se cumpla al genio de tiempos atrás. El genio llega, sin dejarse ver le habla. No puede nada contra uno, y se obtiene lo que se quiera. Probemos.
Movió los muebles hacia la pared, dejando el suelo limpio. Después dibujó sobre el piso, con una tiza, el rombo. Y luego pronunció las palabras: "genio de tiempos atrás concédeme la sabiduría para aprobar geometría ya". El genio se reía de verdad, pero Henry hizo omiso y se llenó de valor y se dispuso a dictar su voluntad.
-Siempre he tenido cero en geometría - empezó.
-A quién se lo dices...- contestó el genio con burla.
Y saltó las líneas para reírse a carcajadas de Henry, las líneas del cuadrado que el muy iluso había dibujado en lugar de un rombo que era el necesario”.
El perímetro del rombo que debía dibujar Henry, tiene una longitud de
14. La gráfica muestra SEIS sitios A, B, C, D, E y F. Si se quiere ir de A hacia F, sin pasar por un sitio más de dos veces, el número de caminos posibles es
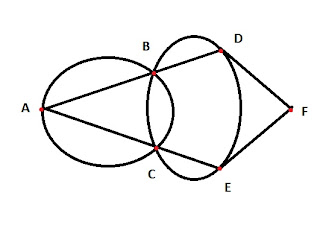Nota: escríbalos, por ejemplo ABDF, ACEF,....
15. El área A de un cuadrado de lado x se calcula mediante la expresión A=6x², al variar de x=1 a x=1,001 se puede establecer que su variación de área con respecto a x es
16. Si A=x2 -4x +6, dA/dx equivale a
17. Si y = 3x² - 6Cos(x) dy/dx equivale a
18. Si y=Ln(x² - 6), y´ equivale a
19. Un globo aumenta su radio r, en centímetros, en función del tiempo t, en segundos, de acuerdo a la ecuación r(t) = 2t²-5t. El volumen V de un globo esférico de radio r se calcula mediante la expresión (búsquela en sus apuntes de clase). La rapidez con la que aumenta su volumen a los 3 segundos es de
20. Si Logx(y)=9, el valor de y' es
21. Derivar el producto x(x-1)(x+3)
22. Calcular ʃ10(x²+3x-1)9(2x+3) dx
23. Calcular ʃ4Sen3(x)Cos(x) dx
24. Calcular ʃCos(x) dx + ʃSen(x) dx
25. Calcular
26 Derivar xLn(x)-x
27 Integrar Ln(x)
28 Derivar xSen(x)
29 Integrar Sen(x) +xCos(x)
30 ¿Qué concluyes de los ejercicios 26 y 27 y de los ejercicios 28 y 29?
31. Calcular el área bajo la curva y=x3 entre x=2 y x=5.
No hay comentarios:
Publicar un comentario