COMASACA, Grado 11, Interpretación de la DERIVADA de una función matemática.

Tema: intepretación gráfica de la derivada de una función.

Propósito: interpretar gráficamente la derivada de una función, identificar su necesidad de creación y reconocer sus aplicaciones en las matemáticas y otras ciencias.

Síntesis histórica de la función derivada

Desde los griegos, se plantearon cuatro problemas fundamentales que al ser resueltos en el s XVI-XVII, dieron vida a la función derivada, fueron ellos: El de la velocidad, el de la recta tangente, el de área bajo una curva y el de máximos y mínimos. Entre los trabajos destacados en la cultura griega, respecto a los procesos de variación se encuentran los de: Zenón de Elea 450 a.C., de la escuela Eleática, para quien el movimiento era imposible y consideraba que el espacio y el tiempo eran infinitamente divisibles. De él son famosas sus paradojas: La del movimiento, la de Aquiles, la de la flecha y la del tiempo. Luego está la escuela de los atomistas:

Leucipio, Demócrito y Jenofonte, s. V y s IV a.C., quienes se preocuparon por atacar el idealismo de la escuela Eleática, centrándose en el otro extremo, el materialismo. Para esta escuela el movimiento correspondía a la interacción de los átomos y de alguna forma concibieron el movimiento como una relación del espacio y el tiempo. En el s. IV a. C aparece Eudoxio, considerado el padre de la astronomía, por lo tanto en su trabajo el movimiento era muy importante. En 370 a. C. logra plasmar su trabajo escrito sobre el método de exhausión, el cual era un método riguroso y esencialmente geométrico de hallar el área bajo una curva a través de polígonos inscritos y circunscritos, logra por este método hallar el área de un círculo. Este método posteriormente fue utilizado por Arquímedes (287-212 a. C.), considerado por algunos como uno de los tres matemáticos más brillantes de la historia, junto con Newton y Gauss, trabajó en matemática pura y aplicada, continuó con el método de exhausión y logró avances significativos en áreas bajo curvas, demostró por series el área de una región de parábola y otras regiones, trabajó en el movimiento y al igual que sus antecesores la intuición fue de vital importancia para su trabajo.

Es evidente que los anteriores nombres hacen parte de los matemáticos griegos que lograron avances significativos en la geometría y en la aritmética, también lo es la dificultad que tuvieron para trabajar con el infinito y el hecho de que si los matemáticos griegos y filósofos como Platón y Aristóteles hubiesen seguido el camino de Arquímedes y no solo el de Euclides, el desarrollo de las matemáticas se hubiese adelantado varios siglos.

Tomado de:
http://www.pedagogica.edu.co/revistas/ojs/index.php/TED/article/viewDownloadInterstitial/261/252

1. Conocimientos previos.

Antes de iniciar, recordemos que se debe tener un nivel satisfactorio en el cálculo de la derivada de una función polinómica por medio del cociente de Newton. En consecuencia, raliza los siguientes ejercicios.


1.1 f(x)=2x-3

1.2 f(x)=5-4x

1.3 f(x)=x(x+1)

1.4 f(x)=x² Solución:



1.5 f(x)= x²-2x+3

1.6 f(x) = x³-x²+x-4

2. Recta tangente a una curva.

Tratemos ahora uno de los problemas de la antiguedad: la recta tangente a una curva. Para iniciar, recordemos las posiciones relativas de una recta en el plano con respecto a una curva dada.

Recta secante a una curva.

Una recta es secante a una curva cuando la corta en dos o más puntos. En la imagen, la recta en color verde es secante a la curva en color azul.

2.1 Ejercicio: marca la opción correcta según el problema que se menciona en la imagen.

Recta tangente a una curva.

La recta secante se transforma en recta tangente cuando los dos puntos de corte se van acercando uno al otro hasta convertirse en uno solo, el punto de tangencia.

Significa que la recta tangente toca a la curva en un solo punto.

¿Dónde radica la importancia de ubicar la recta tangente a una curva?

Veamos gráficamente cómo se comporta la recta tangente a una curva a medida que el punto de tangencia cambia. Recordemos que los puntos altos y bajos de una curva se llaman picos o puntos máximos y mínimos (recordemos que esto fue un problema del siglo XV-XVI que llamó la atención de Pierre Fermat: visitar http://redalyc.uaemex.mx/pdf/695/69520207.pdf, no desde una función como tal sino como un problema geométrico en el cual se debía encontrar un punto P en un segmento AB, tal que el producto de las dos longitudes obtenidas sea el máximo).

Aparte del documento en línea sobre la derivada para Fermat.

Retomando la situación del punto P en un segmento AB, supongamos que el segmento mide 10 cm.

Llamemos M el producto entre AP y PB, entonces:

M = AP PB

M = (y-x) ( x)

M = xy - x²

Como y=10 cm. entonces:

M= x(10) -(10)²

M= 10x-x²

Calculando M(x+h)-M(x)

se tiene:

10(x+h)-(x+h)² - (10x-x²)

10x+10h -(x²+2xh+h²) -10x+x²

10x+10h-x²-2xh-h²-10x+x²

10h-2xh-h²

Dividiendo esto entre h:

10-2x-h

verificando la expresión para h=0 se tiene

10-2x

Como ésta es la fórmula de la pendiente de la recta tangente en cualquier valor de x, se verifica cuándo es cero, así:

10-2x=0

cuando

10=2x

o sea

x=10/2

x=5 cm.

Recuerde que la derivada determina la ecuación de la pendiente de la recta tangente a una curva en cuarlquier punto (x, f(x))

Significa que el punto, según el problema, se debe ubicar en el centro del segmento y que su producto máximo ocurre cuando AP=5cm. y PB=5cm., o sea que M=5cm.(5cm.)=25 cm².

Gráficamente se interpreta como el punto máximo de la gráfica de M=10x-x²


Nótese cono en x=5 ocurre el máximo producto M.


Sabemos ya hoy que la derivada de M con respecto a X en la expresión M=10x-x² es:

M'(x)=10-2x

Al tabular M'(x) para x={0,1,2,3,4,5,6,7,8,9,10} se obtiene:

Se puede notar que la recta tangente toca el punto máximo cuando la pendiente de ésta es cero, esto explica por qué se iguala a cero la derivada para calcular puntos máximos y mínimos, radica en esto la importancia de calcular la ecuación de la recta tangente a la curva.



De acuerdo al mentefacto conceptual se puede deducir que:

2.2 Ejercicio: Escribe las ecuaciones de las rectas que hacen falta en el gráfico.

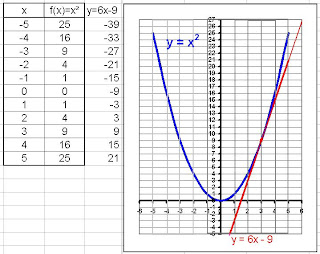
Veamos ahora un problema de origen no geométrico: las rectas tangentes a la curva de ecuación f(x)=x². Su gráfica es:

Calculemos la ecuación de la recta tangente al punto (3,9).

Una recta que pasa por el punto (a,b) y de pendiente m, tiene ecuación:

y-b=m(x-a)

Se conoce que:

a=3
b=9
y que m=f'(x), es aquí donde debemos calcular la derivada de f(x)=x², que según se muestra arriba es:

f'(x)=2x

Por consiguiente,

m=2(3)

m=6

Sustituyendo en la ecuación inicial:

y-b=m(x-a)

y-9=6(x-3)

y-9=6x-18

y=6x-18+9

y=6x-9

Al representar esta ecuación junto con la de f(x)=x², se tiene:


De igual manera para el punto (2,4):

y-b=m(x-a)

como m=2x y x=2 entonces

m=2(2)

m=4

y-4=4(x-2)

y-4=4(x-2)

y-4=4x-8

y=4x-8+4

y=4x-4

Cuya gráfica es:

2.3 Ejercicio: calcule la ecuación de la recta tangente a y=x² en el punto (1,1) y grafíquela

2.4 Ejercicio: calcule la ecuación de la recta tangente a y=x² en el punto (0,0) y grafíquela

2.5 Ejercicio: calcule la ecuación de la recta tangente a y=x² en el punto (-1,1) y grafíquela

2.6 Ejercicio: calcule la ecuación de la recta tangente a y=x² en el punto (-2,4) y grafíquela

2.7 Ejercicio: calcule la ecuación de la recta tangente a y=x² en el punto (-3,9) y grafíquela


3. Derivada de una función aplicada a problemas de distancia, velocidad y aceleración.

La derivada tuvo vida con la solución de problemes sobre velocidad. Por ejemplo, supóngase que una partícula tiene ecuación de moviemiento x= 6t-4t² con x en metros y t en segundos.

Al comparar esta ecuación con la ecuación general X= Xo + Vo t + 1/2 a t², se puede conluir que:

X= 0 + 6t + (-4) t²

X = Xo + Vo t + 1/2 a t²

Por consiguiente, se identifica que:

Xo= 0 m

Vo=6m/s

1/2a=-4

de donde se deduce que a=-8m/s²

Se concluye entonces que se trata de una parícula que viaja con una velocidad inicial de 6m/s y la desacelera a razón de 4m/s cada segundo, con una distancia de ventaja de 0m (cero metros).

¿Cómo conluir esto con ayuda de la derivada?

Grafiquemos x en función de t:

Se evidencia, por ejemplo, que al cabo de 0,75 segundos la distancia que recorre es de 2,25 metros, la máxima alcanzada. Este es un movimiento que si se tabula para tiempos de 1, 2, 3.. segundos, no se obtiene una gráfica explícita.

¿Cómo saber qué valores darle al tiempo, a partir de la ecuación x=6t-4t² ?

¿Cómo identificad de manera analítica que la velocidad inicial es 6 y que la aceletración es de -8m/s²?

Para esto, recordemos que la velocidad se define como la variación del desplazamiento por unidad de tiempo. Por ejemplo, para tiempos entre t1=0 seg y t2= 0,1 seg, la partícula se desplazo de una posición:

X( t1 ) = 6( t1 )-4( t1 )²

X(0 ) = 6(0 )-4(0 )²

X( 0 ) = 0 -4(0)
x(0) = 0 m.

y para t2

X( t2 ) = 6( t2 )-4( t2 )²

X(0,1 ) = 6(0,1 )-4(0,1 )²

X(0,1 ) = 0,6 -4(0,01 )

X(0,1 ) = 0,6 -0,04

X(0,1 ) = 0,56

Como la velocidad equivale a:

Se tiene que:

Que es un valor cercano a 6m. Para mayor precisiòn, calculemos para t1=0 seg y t2= 0,01 seg, es decir un intervalo de tiempo más pequeño.


Significa que entre más pequeña sea la diferencia entre los tiempos, más pequeña es la diferencia entre los desplazamientos. Al dividir estos dos resultados el límite de esa relación entre las diferencias es de 6m/seg. Nótese que en el elemento x(t+h), la h equivale a 0,01.

Significa que al calcular
Se obtiene la expresión:

X'(t) = 6 - 8t
Que es la ecuación de velocidad de la partícula en un determinado tiempo t, ya que para t=0.01,

x'(t) = 6-8(0.01)

x'(t) = 6-0.08

x'(t) = 5,92m/seg

O para t=0.001, se tiene:

x'(t) = 6-8(0.001)

x'(t) = 6-0.008

x'(t) = 5,992m/seg

Que evidentemente se aproxima a 6 m/seg

Nótese que la aceleración ya se ve en la ecuación X'(t) = 6 - 8t.

Si a esta expresión le llamamos V(t), queda:

v(t)=6-8t

Pues es la velocidad en función del tiempo, también llamada ecuación de la velocidad de la partícula.

Ahora, si derivamos rapidamente esta ecuación, se obtiene v'(t)= -8, que es la aceleración de la que habíamos hablado lineas atrás.

En resumidas cuentas, al derivar la ecuación de x--t (leáse x en función de t), se obtiene la ecuación de v--t y si derivamos la ecuación de v--t, se obtiene la ecuación de la aceleración de la partícula en función del tiempo.

3.1 Ejercicio: La ecuación del movimiento de una partícula está dada por la expresión

x(t)= 50t-200t² (x en metros y t en segundos):

3.1.1 Graficar x --t e indicar valores de t para los cuales x es cero y máximo.

3.1.2 Escribir la ecuación de la velocidad. ¿Qué velocidad experimenta al cabo de 4 segundos?

3.1.3 Escribir la ecuación de la aceleración. ¿Qué aceleración experimentó durante todo el movimiento?


3.2 Ejercicio: La ecuación del movimiento de una partícula está dada por la expresión

x(t)=(t-4) (t-2) (15-t) (x en metros y t en segundos):



3.2.1 Graficar x --t e indicar valores de t para los cuales x es cero y máximo. Nota: tabule de 0 a 15 segundos.

3.2.2 Escribir la ecuación de la velocidad. ¿Qué velocidad experimenta al cabo de 3 segundos? ¿Qué velocidad experimenta al cabo de los 11 segundos?

3.2.3 Escribir la ecuación de la aceleración. ¿Qué aceleración experimenta al cabo de 5 segundos? ¿Es la aceleración constante en todo el movimiento?

3.2.3 ¿Cuál es el valor mínimo de la distancia x entre 2 y 4 segundos, para qué tiempo ocurre? ¿Cuál es la distancia máxima entre 4 segundos y 15 segundos, para qué tiempo ocurre?

3.2.4 Realice un gráfico de velocidad en función del tiempo y construya sus propias conclusiones.

3.2.5 Relice un gráfico de aceleración en función del tiempo y construya sus propias conclusiones.

"Diría todo lo que sé por la mitad de lo que ignoro".

René Descartes.