Grado 10º Ley Seno y Ley Coseno Taller de refuerzo Presentación Aguacatal.

Al revisar las evaluaciones escritas y observar que de 30 estudiantes, el 16% obtiene un nivel entre básico y superior, me pregunto ¿qué pasó? Busco varios factores relevantes para dar respuesta a la pregunta y analizo desde varios puntos de vista la situación.

La primera mirada se dirige a la manera como se abordó el tema desde mi orientación como profesor: ¿cómo estuvieron las explicaciones y ejemplos dados? ¿Fueron suficientes estas explicaciones? ¿se aplicó el método adecuado? ¿Las transposiciones realizadas para el tema fueron acertadas?

Ahora se debe buscar en la estudiante: ¿qué te preguntarías?

Parte I

Acciones de Mejora

El primer ejercicio en este taller es responder a las siguientes preguntas que escudriñan acerca de tus actitudes y aptitudes frente al tema de ley de Seno y Coseno.

De acuerdo con la siguiente escala de valoración, indique al frente de cada situación el nivel que usted presentó en las clases ofrecidas para el tema.

1-> Bajo
2->Básico
3-> Alto
4->Superior

1. Comportamiento de atención que presenté en las clases ( )
2. Conocimientos previos relevantes para su comprensión ( )
3. Realización de talleres para afianzar ( )
4. Profundización en el tema por su cuenta ( )
5. Explicaciones adicionales pedidas ( )
6. Cumplimiento con materiales en clase ( )
7. Gusto por la exploración en matemáticas ( )

Reflexione sobre los resultados obtenidos, realice un diagrama de Pareto y establezca los pocos vitales en los cuales usted va a aplicar acciones de mejora.

Parte II

Ahora escudriñemos mas en la evaluación escrita que se hizo.

Se realizó el lunes 15 de febrero de 2010, en la primera y segunda hora del horario del día, en horario especial cuya hora dura 45 minutos (normalmente tienen una duración de 50 minutos). Se realizó en el salón (no se ubicaron afuera en el corredor y con distancia prudente como en las pruebas "acumulativas"). Se debía tener calculadora. Constaba de ocho preguntas en donde siete de ellas aparecia el triángulo o gráfico dibujado en el tablero con las respectivas medidas necesarias y con el enunciado: "resolver cada situación". Fue necesario aclarar que resolver un triángulo significaba hallar la medida de todos sus lados y ángulos.


Descripción de los problemas:

Los problemas 1 y 2 eran dos triángulos rectos el primero de hipotenusa 200 metros y uno de sus ángulos agudos de 40°, el segundo tenía uno de sus catetos de longitud 400 metros y ángulo opuesto de 60° .

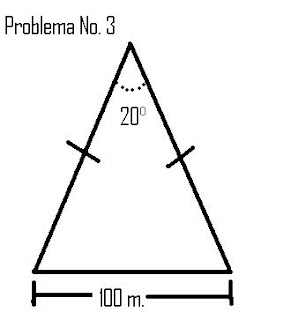
El problema tercero era un triángulo ABC con ángulo A de 20 grados y lado a de 100 metros de longitud. La figura en el tablero indicaba que los lados AB y AC tienen la misma longitud.













El cuarto problema era un triángulo ABC no recto (oblícuo) con AC=100, AB=200 y el ángulo entre estos dos lados de longitud conocida de 30 grados.














El quinto problema no presentaba gráfico, consistía aplicar la ley de Coseno a un triángulo equilátero. No proponía sacar conclusiónes, lo dejé a su iniciativa buscar sus inferencias.













El sexto problema era un triángulo con dos ángulos internos de 20 grados y uno de los lados opuesto a uno de estos ángulos de medida 40 metros.















El séptimo problema era hallar el perímetro de un trapecio recto (así se indicaba en el gráfico) de bases mayor 100 metros y base menor 40 metros con ángulo agudo de 60°.













Y el octavo y último problema (situación para pensar o desafío cognitivo) consitía en hallar el perímetro de un cuadrilátero en donde dos lásod contíguos miden 30 y 40 con ángulo entre ellos de 100 grados y el otro lado contíguo al de 40 metros con una longitud también de 40 metros. El ángulo opuesto al de 100 grados mide 80 grados.

Al hacer estas descripciones del problema, cabe resaltar que el nivel de dificultad de la evaluación es menor cuando se dá el esquema o representación gráfica del problema, puesto que parte de este está resuelto.

Teniendo la claridad de cada problema en cuanto a su descripción, respondamos de manera tranquila y reflexiva las siguientes preguntas:

1. Al resolver el primer problema, sus dificultades fueron:

(a) Poca claridad en la figura
(b) Desconocer que se trataba de un triángulo recto.
(c) Olvidar o no tener práctica de aplicar la propiedad de la suma de los ángulos internos de un triángulo cuyo total es 180 grados.
(d) Desconocer un lado y su ángulo opuesto
(e) Desconocer cuál ley aplicar si la de senos o cosenos.
(f) Olvidar la fórmula de ley de senos
(g) Identificar la proporción de la ley de senos que sirve para hallar el lado o ángulo pedido.
(h) Despejar la incógnita en la proporción planteada en la ley de senos.
(i) Hallar los resultados con la calculadora.



2. Al resolver el segundo problema, sus dificultades fueron:

(a) Poca claridad en la figura
(b) Desconocer que se trataba de un triángulo recto.
(c) Olvidar o no tener práctica de aplicar la propiedad de la suma de los ángulos internos de un triángulo cuyo total es 180 grados.
(d) Desconocer un lado y su ángulo opuesto
(e) Desconocer cuál ley aplicar si la de senos o cosenos.
(f) Olvidar la fórmula de ley de senos
(g) Identificar la proporción de la ley de senos que sirve para hallar el lado o ángulo pedido.
(h) Despejar la incógnita en la proporción planteada en la ley de senos.
(i) Hallar los resultados con la calculadora.


3 Al resolver el problema tercero, sus dificultades fueron:

(a) Poca claridad en la figura
(b) Desconocer que se trataba de un triángulo isósceles y que por ende tiene dos ángulos internos congruentes (de igual medida).
(c) Olvidar o no tener práctica de aplicar la propiedad de la suma de los ángulos internos de un triángulo cuyo total es 180 grados.
(d) Desconocer un lado y su ángulo opuesto
(e) Desconocer cuál ley aplicar si la de senos o cosenos.
(f) Olvidar la fórmula de ley de senos
(g) Identificar la proporción de la ley de senos que sirve para hallar el lado o ángulo pedido.
(h) Despejar la incógnita en la proporción planteada en la ley de senos.
(i) Hallar los resultados con la calculadora.


4. Al resolver el cuarto problema , sus dificultades fueron:

(a) Poca claridad en la figura
(b) Desconocer de qué tipo de triángulo se trataba.
(c) Olvidar o no tener práctica de aplicar la propiedad de la suma de los ángulos internos de un triángulo cuyo total es 180 grados.
(d) Desconocer un lado y su ángulo opuesto
(e) Desconocer cuál ley aplicar si la de senos o cosenos.
(f) Olvidar la fórmula de ley de coseno.
(g) Identificar la proporción de la ley de coseno que sirve para hallar la longitud del lado o ángulo pedido.
(h) Despejar la incógnita en la proporción planteada en la ley de cosenos.
(i) Hallar los resultados con la calculadora.


5. El quinto problema no tenía gráfico. Consistía en aplicar la ley de Coseno en un triángulo equilátero. Estaba en su iniciativa y creatividad matemática, calro que también la exeriencia juega aquí un papel relevante, el proceso de solución y desarrollo del mismo, para llegar a concluir que los ángulos internos de éste tipo de triángulo son congruentes y tienen una medida de 60°.

Al resolver el quinto problema , sus dificultades fueron:

(a) Poca claridad en el enunciado.
(b) Desconocer de qué tipo de triángulo se trataba y cómo se dibujaba.
(c) Olvidar o no tener práctica de aplicar la propiedad de la suma de los ángulos internos de un triángulo cuyo total es 180 grados.
(d) Desconocer un lado y su ángulo opuesto en un triángulo.
(e) Confundir la ley de senos con la de coseno.
(f) Olvidar la fórmula de ley de coseno.
(g) Identificar la proporción de la ley de coseno que sirve para hallar la longitud del lado o ángulo pedido.
(h) Despejar la incógnita en la proporción planteada en la ley de cosenos.
(i) No generalizar, olvidando asumir cada lado como de longitud desconocida x o cualquier incógnita, lo mismo para los ángulos.
(j) Hallar los resultados con la calculadora.


6. Al resolver el sexto problema, sus dificultades fueron:

(a) Poca claridad en la figura
(b) Desconocer que se trataba de un triángulo isósceles por los dos ángulos congruentes de 20 grados cada uno y que por ende tiene dos lados de igual medida.
(c) Olvidar o no tener práctica de aplicar la propiedad de la suma de los ángulos internos de un triángulo cuyo total es 180 grados.
(d) Desconocer un lado y su ángulo opuesto
(e) Desconocer cuál ley aplicar si la de senos o cosenos.
(f) Olvidar la fórmula de ley de senos
(g) Identificar la proporción de la ley de senos que sirve para hallar el lado o ángulo pedido.
(h) Despejar la incógnita en la proporción planteada en la ley de senos.
(i) Hallar los resultados con la calculadora.


7. A cambio de un triángulo, se ofreció una figura en forma de trapecio recto, donde se daban las medidas de sus bases mayor y menor y la medida de su único ángulo agudo.

(a) Poca claridad en la figura
(b) Desconocer que se trataba de un trapecio, que era recto y que tiene bases, un ángulo agudo, uno obtuso y dos rectos.
(c) Olvidar o no tener práctica de aplicar la propiedad de la suma de los ángulos internos de un cuadrilátero, cuyo total es 360 grados.
(d) Desconocer que esta figura está formada por un rectángulo y un triángulo recto.
(e) Desconocer cuál ley aplicar si la de senos o cosenos en el triángulo obtenido.
(f) Olvidar la fórmula de ley de senos
(g) Identificar la proporción de la ley de senos que sirve para hallar el lado o ángulo pedido.
(h) Despejar la incógnita en la proporción planteada en la ley de senos.
(i) Tener poca habilidad en la separación de la figuras y la manera como se identifican los nuevos segmentos y sus medidas.
(j) Hallar los resultados con la calculadora.

8. Al resolver el octavo problema, sus dificultades fueron:

(a) Poca claridad en la figura
(b) Desconocer que se trataba de un cuadrilátero que se pude dividir en dos triángulos por medio de una de sus diagonales para trabajar cada uno por separado.
(c) Olvidar o no tener práctica de aplicar la propiedad de la suma de los ángulos internos de un cuadrilátero, cuyo total es 360 grados.
(d) No llegar a la decisión creativa de trazar la diagonal para relacionar un triángulo con el otro.
(e) Desconocer cuál ley aplicar si la de senos o cosenos en el triángulo obtenido.
(f) Olvidar la fórmula de ley de coseno.
(g) Despejar la incógnita en la proporción planteada en la ley de senos.
(h) Tener poca habilidad en la separación de la figuras y la manera como se identifican los nuevos segmentos y sus medidas.
(i) Hallar los resultados con la calculadora.


Para finalizar, analice el grupo de dificultades en cada problema, revise cuales son comunes en ellos y establezca un plan de mejora frente a esta situación. Proponga a continuación los aspectos que usted debe fortalecer, según el análisis anterior:

1.

2.

3.

4.

5.

6.

Parte III

Como se ha planteado en la metodología en matemáticas, después de esto se debe realizar una recuperación de logros. Para esto propongo a continuación una serie de ejercicios para que usted potencialice procesos y afiance conocimientos. Se debe presentar como se ha convenido en clase.

1. Construya un triángulo ABC con AB= 8 cm. con ángulo A de 50 grados y ángulo B de 40 grados. Mida las longitudes de los otros dos lados y calcule la medida del otros ángulo. Luego aplique la ley de seno o coseno, según convenga, para verificar los resultados experimentales obtenidos.

2. Ubique los siguientes segmentos con un extremo en el origen del plano y halle la distancia entre sus otros dos extremos: Segmento AB con B(5,6) y segemnto CD con D(1,8) Haga uso de su creatividad y las herramientas de geometría.

3. Dos vehículos de igual masa chocan uno con otro de tal manera que después de esto quedan juntos. Si el primero viaja a 40km/h en dirección 10 grados Norte Oeste (NO) y el otro a 70 grados NO. Trace la trayectoria que los vehículos siguen y calcule la velocidad de los dos cuerpor adheridos.

4. Demuestre que las diagonales de un cuadrado se cruzan formando un ángulo de 90 grados.

5. Un rectángulo de dimensiones a por b tiene unas diagonales que se cruzan fromando un ángulo agudo m, escriba una expresión trigonométrica que relacione a y b con m.

6. Un rombo tiene lados de longitud x, su ángulo agudo mide m y el obtuso n, halle el área del rombo en téminos de m, n y x.

7. Sea PQR un triángulo recto en P, establezca la ley de coseno sobre el ángulo recto. ¿Qué concluye?

8. Sea i el ángulo interno de un pentágono regular, calcule su área sabiendo que su lado mide m centímetros.

9. Dibuje una circunferencia de radio r, incsriba en ella un triángulo escaleno de lados a, b y c. Aplique la ley de Seno a cada uno de los tres triángulos isósceles que se forman con los radios de la circunferencia y luego aplíquelo para el triángulo grande. Relacione las ecuaciones obtenidas. ¿Qué concluyes? Consulte en internet cómo está relacionado el radio de una circunferencia con los lados de un triángulo inscrito en ella.

10. Hallar el radio de la circunferencia circunscrita a un triángulo de lados 4, 5 y 6 cm. Constrúyalo si es necesario.

Espero este proceso reflexivo y crítico del instrumento de evaluación haya sido de gran aporte para ustedes.

Por último, una página que les ayudará a recordar algunas cosas
http://personal5.iddeo.es/ztt/For/F7_Triangulos.htm