Deben presentar estos ejercicios para el lunes 08 de julio. La evaluación corregida, y de los puntos que no tienen ejercicios, diseñar de cada uno tres y solucionarlos. Deben presentar una autoevaluación donde indiquen los factores relevantes por los cuales no aprobaron la evaluación.
Los resultados:
9-B Sólo la aprobó Karol Guerra con un 50%
9-A Sólo la aprobaron Paula Andrade, Daniela Charria y Daniela Velez con una maravillosa E.
¡Qué hacer? Pues corregir y practicar más. Hay indicios en la evaluación que me llevan a concluir que NO estudiaron la mayoría.
1. Daniel tiene 30 hojas y Camilo sólo 10, ¿cuántas hojas le debe dar Daniel a Camilo para que al final tengan la misma cantidad?
Solución: Si tiene 30 Camilo y Daniel sólo 10, Camilo le da 10 a Daniel y ambos quedan con 20. A manera de ecuación sería:
Sea x lo que Camilo le da a Daniel,
30-x cantidad de hojas con las que queda Camilo
10+x Cantidad de hojas con las que queda Daniel
Se igualan pues se quiere que queden con la misma cantidad de hojas.
30-x= 10+x
30-10=x+x
20 = 2x
20
--- = x
2
x= 10
Se valoraba también el símple análisis por ensayo error (e/e)
2. Los lados opuestos de un rectángulo miden a y b centímetros. Calcular su perímetro P y su área A. Hacer la representación gráfica.

Solución: El perímetro es la suma de las longitudes de todos sus cuatro lados.
P=a+b+a+b= a+a + b +b = 2a+2b
Su área es el producto de la longitud de su base a por su altura b.
A= ab
3. Resulta curioso ver que (5+6)² es equivalente a 5²+2(5)(6)+6². Muchos cometen el error de omitir en el cálculo la parte de 2(5)(6). En general, (a+b)²=a²+2ab+b². De acuerdo con esto, calcular (12+13)² mostrando el proceso.
Solución:
(12+13)² = 12² + 2(12)(13) + 13²
144 + 24(13) + 169
144 + 312 + 169
625
Si la quieren verificar, sólo basta con sumar 12 y 13 para obtener 25, y luego calcular 25² que equivale a 25 por 25 = 625
La mayoría de las niñas cometieron el error de multiplicar, en la expresión 2(12)(13), el 2 por 12 y también por el 13, desconociendo que la multiplicación no es distributiva con respecto a ella misma. En resumidas cuentas el 2 sólo multiplica al 12 y no al 13 ó si deseas que sólo multiplique al 13 y NO al 12. En síntesis, multiplica sólo a uno de los factores, pero no a ambos.
4. Cuando multiplicamos una cantidad a+b pos su conjugado a-b, se obtiene a²-b², demuestre esto realizando el producto.
Solución: Se pide caclular el producto algebraico entre
(a+b)(a-b)
aa -ab +ab -bb Aplicando la propiedad distributiva de la suma con respecto al producto.
a² +0ab -b² Simplificando términos semejantes.
a² - b² omitiendo el termino nulo 0ab
Ejercicios: Cuando un estudiante no hace este tipo de producto, se recomienda que practique productos sencillos como:
(01) 3x(4x)
(02) 6ab(-2ab²)
(03) -3x²y³(4xy)(2x)
Hasta aquí productos de monomio monomios.
(04) 4(2a-3b+4c)
(05) 6x(-2x²+3x-8)
(06) 0,5r²(3x-r)
Hasta aquí producto de monomio polinomio
(07) (2x+3)(3x+1)
(08) (6m-1)(6m+1) Producto notable suma por diferencia representativo de este problema 4.
(09) (4x²-8y)(3x+2y-100)
Hasta aquí productos binomio polinomio
(10) (a+b)(a+b) No confundir con (a+b)(a-b)
(11) (2x+4)(2x+4) Recuerde que tambien puede aparecer como (2x+4)²
(12) (x-1)(x-1)
(13) (√2 +4)(√2+4) Una ayudita ....
(√2)² +2(√2)(4) + (4)² Recuerde que (√2)² da √4 = 2
(14) (x+√x) (x-√x) Aquí los terminos del centro se cancelan!
(15) Una situación para pensar: Un cuadrado tiene su lado de longitud x, si todos se disminuyen en 4 centímetros, ¿en cuánto se disminuye su área? Recuerde representar graficamente la situación.
Respuesta: se disminuye en (-8x+16) cm²
5. El texto en esta pregunta se referia al proceso de dividir el perímero (P:perímetro) de la circunferencia en su diámero (D: diámetro, r: radio entonces D=r+r es decir D=2r)
Se afirma que:
p
-- = π
DEsto significa que cualquier circunferencia de longitud p, al dividirla entre su diámetro, se obtiene 3 "pedazos" y un poco más, a este número que no es racional sino irracional, se le denominó π (de periphereia).
Información tomada de http://www.portalplanetasedna.com.ar/numero_pi.htm
Despejando p se tiene: p= D π, que responde a la pregunta, es decir que la opción a:"Pi veces el diámetro" es la correcta. Para profndizar un poco, como D=2r, se tiene que
p= (2r) π
p= 2 πr
Ejercicios:
(01) En la ecuación p= 2 πr, despejar r.
(02) En la ecuación A= πr², despejar r.
(03) Calcular el perímetro (en metros) de un círculo cuyo radio mide 30cm.
Nota: recuerde convertir los 30cm en metros, aplique el método de conversión de datos, que se apoya en el inverso multiplicativo de una cantidad.
(04) Calcular el área de un círculo cuyo radio mide √5 cm.
Nota: recuerde que (√5)² equivale a 5.6. Se debe poner una cinta roja en el borde de una mesa circular de radio 60 cm. Si el metro de esta cuesta $1.000, ¿ cuál es el costo de la cinta para este trabajo?
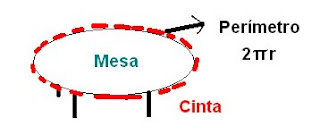
Solución: Como p=p= 2 πr, se tiene que:
p= 2 π (60cm), pero la respueta la piden en m, entonces:
p= 2 π (60cm) (1m/100cm)
p= 2 π (0,6m)
p= 1,2 πm, ahora como el valor del metro lineal de cinta es $1000, su costo es:
Costo= 1,2 πm ($1.000)/m, se cancela m con m y queda:
Costo= $1.200 π
Se pidió dejar indicado el numero pi, pues no se debía usar caculadora.
7. Elevar al cuadrado el binomio (x+y), es decir calcular (x+y)²
Solución:
(x+y)²
= (x+y) ( x+y)
= xx + xy + yx + yy
= x² + 2xy + y²
Ejercicios:
(01) Sea f(x) = x²-5x+6, calcular f(1) + f(-1)
(02) Escribir el área de un círculo cuyo radio mide x+3y unidades.
(03) La energía cinética de un cuerpo de masa m que lleva una velocidad V se calcula mediante la expresión:
E = 1/2 mV². Las unidades de la masa en kg y la velocidad en m/s, para obtener julios.
Calcular E, en julios, si el móvil tiene una masa de 1.000kg y una velocidad de 40m/s
8. El radio de un cículo mide m+n, calular su área A en función de m y n.
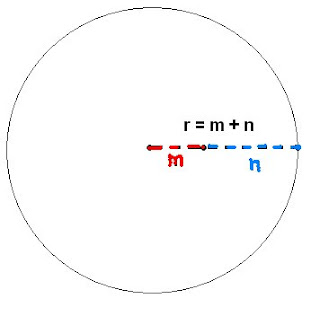
Solución:
A= πr²
A= π(m + n)²
A= π(m² +2mn + n²) ó puede escribirse también
A= πm² +2πmn + πn² .
9. Sea y= 5(x-2)² + 4 la ecuación explícita de una parábola, escríbala de la forma general (y=ax²+bx+c).
Solución: lo que se pide es efectuar el binomio al cuadrado y simplificar la expresión
y= 5(x-2)² + 4
y= 5(x²-4x+4)² + 4
y= 5x²-20x+20 + 4
y= 5x²-20x+24
y= 5x²+(-20)x+24
Vemos que a = 5, b = -20 y c = 4
10. Calcular la media, mediana u moda de los siguientes datos 3, 4, 3, 5, 6, 7, 8, 9, 10, 10, 4, 6, 5, 7, 7, 8, 5 y 4.
Solución: para todos los calculos, se tiene que el número de datos es 18, o sea que n=18.
Media = 111/18 = 6,16
Mediana: era necesario organizar los datos, la mayoría de las estudiantes no lo hicieron.
3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7 , 7, 7 , 8, 8, 9 ,10 y 10
la mediana se calcula con el promedio de los datos X9 y X10,
Mediana= (6+6)/2 = 12/2 = 6
Moda: vemos que los datos 4, 6 y 7 tienen la misma frecuencia de 3, como es el dato que más se repite, decimos que es trimodal.
11. Escribir de la forma y=a(x-h)² +k, la expresión y=2x²+4x+6.
Solución:
y=2x²+4x+6.
y/2 = 2/2 x² + 4/2 x + 6/2.
y/2 = 1 x² + 2 x + 3.
y/2 = x² + 2 x + 3.
y/2 = x² + 2 x + (2/2)² - (2/2)² + 3.
y/2 = x² + 2 x + (1)² - (1)² + 3.
y/2 = (x + 1)² - (1)² + 3.
y/2 = (x + 1)² - 1 + 3.
y/2 = (x + 1)² + 2.
y/2 = (x + 1)² + 2.
y= 2 (x + 1)² + 2(2).
y= 2 (x + 1)² + 4.
y= 2 (x -(-1) )² + 4.
Ejercicios: Escribir de la forma general
(01) y= x²+6x + 4.
(02) y= x²-6x + 4.
(03) y= 10x²+6x + 16.
(04) y= 3x²-6x + 12.
(05) y= 5x²-20x -100.
(06) y= 5x²-2x -1.
(07) y= √5 x²-2x -10.
12. Simplificar el radical √(4x²y³z²)
Solución:
√(4x²y³z²)
√(2² x² y² y¹ z²)
√2² √x² √y² √y¹√ z²
2 x y √y¹ z
2 x y z √y¹
2 x y z √y
13. Calcular (1 + √3 ) (5-2√3)
Solución:
(1 + √3 ) (5-2√3)
1 (5-2√3) + √3 (5-2√3)
5 - 2√3 + 5√3 - 2√3²
5 - 2√3 + 5√3 - 2√9
5 + 3√3 - 2(3)
5 + 3√3 - 6
5-6 + 3√3
-1 + 3√3
14. Racionalizar 5/ (10- √3)
Solución:
5/ (10- √3)
= 5(10+ √3) / (10- √3)(10- √3)
=(50+ 5√3) / (10² - (√3)²)
=(50+ 5√3) / (100 - √9)
=(50+ 5√3) / (100 - 3)
=(50+ 5√3) / 97
=50/97 + (5/97) √3
Y hasta aquí la solución de la evaluación para 9-B, que le sirve a ambos.

No hay comentarios:
Publicar un comentario