Un vehículo consume 5 galones de gasolina en un trayecto de 200 km. de sistancia.
Galones........ Distancia (Km.)
5----------- 200
Significa que las dos carreteras están separadas 90 metros.
Actividad 4: Calcular el valor de la incógnita a partir de la información suministrada en el grafico. Plantee la ecuación en forma de proporción y despeje la incógnita.
4.1.
4.2. 
4.3.
Concentraremos nuestra atención en aquellas proporciones que resultan de la solución de triángulos rectos.
Nótese que la proporción se reescribe intercambiando el 10 y el 20, es decir, intercambiando los medios de la proporción. De esta manera se obtiene la razón entre cateto opuesto e hipotenusa, llamada razón trigonométrica Seno (Sinus en latín, que significaba Bahía o entrada).
Recordemos un poco cómo identificar el cateto opuesto (Co), el adyacente (Ca) y la hipotenusa (Hip). Recuerde que el Ca se denota con la letra "x", el cateto opuesto Co con la letra "y" y la hipotenusa con la letra "r".
Actividad 5: Identificar Co, Ca e hipotenusa en cada triángulo, ubicando en cada lado la letra que le corresponde.
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
La razón trigonométrica Seno se calcula mediante la relación entre la longitud del cateto opuesto sobre la longitud de la hipotenusa:
La reazón trigonométrica Coseno se calcula mediante la relación entre la longitud del cateto adyacente y la hipotenusa:
La razón trigonométrica Tangente se calcula mediante la relación o división entre el cateto opuesto y el cateto adyacente:
Actividad 6: Establezca las razones Seno, Coseno y Tangente de alfa para cada uno de los triángulos del ejercicio anterior. Dibuje el triángulo de nuevo y al lado derecho escriba las razones.
Si dos triángulos rectos son semejantes, la razón Seno del ángulo congruente resulta equivalente, de igual manera para Coseno y Tangente.
Actividad 7. Calcular el valor de la hipotenusa o cateto opuesto, planteando la razón Seno.
7.1
7.2
Actividad 8: Establezca la razón Seno de alfa, obteniendo así la ecuación en forma de proporción y despeje la incógnita.
8.1
8.2
8.3
8.4 
8.5
Actividad 9: Establezca la razón coseno de alfa y despeje la incógnita.
9.1
9.2
9.3
9.4
Actividad 10: Solucione el triángulo rectángulo en términos del ángulo de referencia. Cuando tenga despejada la incógnita, haga uso de la calculadora para encontrar el valor de seno o coseno del ángulo pedido.
10.1
10.2
10.3
10.4
Actividad 11: Establezca la razón trigonométrica Tangente en los triángulos del punto 10, es necesario que dibuje el triángulo de nuevo.
Actividad 12: Resolver, construyendo el triángulo que es necesario par la mejor comprensión del problema.
12.1 Un poste de 10 metros de altura es amarrado al piso por medio de una cuerda que forma un ángulo de 45 ° con la horizontal. ¿Qué longitud tiene la cuerda?
12.2 La sombra de un edificio, en un momento del día, forma un ángulo de 20° con la horizontal. Si la sombra mide 50 metros, ¿qué altura tiene el edificio?
12.3 Una rampa tiene un altura de 50 cm, y forma un ángulo de 30° con la pared. ¿Qué ángulo forma con el piso y qué longitud de rampa tiene?
Fin del Taller.
5----------- 200
Surge la necesidad de conocer la distancia que se puede alacanzar con sólo 1 galón. Para esto se realiza una comparación en forma de cociente, entre las dos magnitudes: Capacidad en galones y distancia que recorre.
Galones ......Distancia (Km.)
5 -----------200
Resulta obvio que la quinta parte de la cantidad de galones alcanzará par la quinta parte de la distancia, es decir:
De acuerdo con esto, la razón entre 80 y 20 debe dar lo mismo que la razón entre x+30 y 30, escrito en forma de proporción sería:
De donde
80 (30) = 20(x+30)
Producto de medios con extremos.
2400 = 20x+600
Despejando la incógnita de la ecuación resultante.
2400-600=20x
1800=20x
90=x
Resulta obvio que la quinta parte de la cantidad de galones alcanzará par la quinta parte de la distancia, es decir:
Galones ..........Distancia (Km.)
5/5 ---------- 200/5
1 ------------40
Significa que 1 galón alcanza para 40 kilómetros.
Es necesario resaltar que al establecer el cociente entre distancia y capacidad en galones, también se obtiene 40 km/gal.
En resumen, las razones en matemáticas se usan para comparar dos o más magnitudes.
Actividad 1: Calcular la razón entre las dos magnitudes que se mencionan.
1.1 5 litros de leche cuestan $12.000
1.2 Una persona descubre que durante 60 segundos su corazón late 80 veces.
1.3 Una persona recorre 20 km en media hora.
1.4 Un computador procesa 1 millón de letras en tan sólo 0,001 segundo.
1.5 Un triángulo recto tiene una hipotenusa de longitud 15 cm cuando se amplió al triple.
Actividad 2: Resolver los siguientes problemas:
2.1 Un vehículo viaja a razón de 40 kilómetros por hora, ¿en cuánto tiempo recorre 300km.?
2.2 Una persona normal puede leer 3 palabras por segundo, ¿cuánto tarda en leer 600 palabras?
2.3 Por un grifo de agua salen 6 litros de agua por minuto, ¿qué cantidad de agua sale en una hora?
2.4 La razón entre la altura y la base de un triángulo recto es 3/4, ¿calcular su altura si la base es 8 cm.?
Actividad 3: Identificar la razón entre las dos magnitudes que se muestran en la figura.
3.1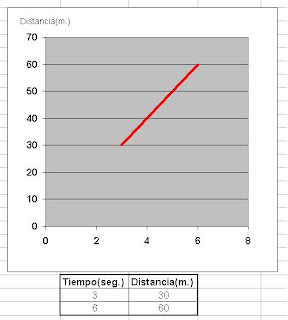
3.2
Como se puede notar, la distancia entre el punto B y la carretera de 20 m es de 30m, y la distancia entre la carretera de 20m y 80 m. es desconocida y la llamaremos X.1 ------------40
Significa que 1 galón alcanza para 40 kilómetros.
Es necesario resaltar que al establecer el cociente entre distancia y capacidad en galones, también se obtiene 40 km/gal.
En resumen, las razones en matemáticas se usan para comparar dos o más magnitudes.
Actividad 1: Calcular la razón entre las dos magnitudes que se mencionan.
1.1 5 litros de leche cuestan $12.000
1.2 Una persona descubre que durante 60 segundos su corazón late 80 veces.
1.3 Una persona recorre 20 km en media hora.
1.4 Un computador procesa 1 millón de letras en tan sólo 0,001 segundo.
1.5 Un triángulo recto tiene una hipotenusa de longitud 15 cm cuando se amplió al triple.
Actividad 2: Resolver los siguientes problemas:
2.1 Un vehículo viaja a razón de 40 kilómetros por hora, ¿en cuánto tiempo recorre 300km.?
2.2 Una persona normal puede leer 3 palabras por segundo, ¿cuánto tarda en leer 600 palabras?
2.3 Por un grifo de agua salen 6 litros de agua por minuto, ¿qué cantidad de agua sale en una hora?
2.4 La razón entre la altura y la base de un triángulo recto es 3/4, ¿calcular su altura si la base es 8 cm.?
Actividad 3: Identificar la razón entre las dos magnitudes que se muestran en la figura.
3.1
3.2
Las razones en los triángulos rectos.
Cuando se habla de razon en un triángulo recto, se hace referencia al cociente entre las longitudes de dos de sus lados, con el propósito de resolver un problema geométrico que implica semejanza de figuras planas.
La razón más común es la que se establece entre lados correspondientes. Recordemos que dos lados de un triángulo son correspondientes cuando la medida de sus ángulos adyacentes es la misma. Por ejemplo en la gráfica de abajo al segmento que representa la carretera de 80m. le corresponde la el segmento que representa la carretera de 20 m., siendo las dos carreteras paralelas. Según la información ¿qué distancia separa las dos carreteras?
De acuerdo con esto, la razón entre 80 y 20 debe dar lo mismo que la razón entre x+30 y 30, escrito en forma de proporción sería:
De donde80 (30) = 20(x+30)
Producto de medios con extremos.
2400 = 20x+600
Despejando la incógnita de la ecuación resultante.
2400-600=20x
1800=20x
90=x
Significa que las dos carreteras están separadas 90 metros.Actividad 4: Calcular el valor de la incógnita a partir de la información suministrada en el grafico. Plantee la ecuación en forma de proporción y despeje la incógnita.
4.1.
4.2. 
4.3.
Concentraremos nuestra atención en aquellas proporciones que resultan de la solución de triángulos rectos.
Nótese que la proporción se reescribe intercambiando el 10 y el 20, es decir, intercambiando los medios de la proporción. De esta manera se obtiene la razón entre cateto opuesto e hipotenusa, llamada razón trigonométrica Seno (Sinus en latín, que significaba Bahía o entrada).
Recordemos un poco cómo identificar el cateto opuesto (Co), el adyacente (Ca) y la hipotenusa (Hip). Recuerde que el Ca se denota con la letra "x", el cateto opuesto Co con la letra "y" y la hipotenusa con la letra "r".
Actividad 5: Identificar Co, Ca e hipotenusa en cada triángulo, ubicando en cada lado la letra que le corresponde.
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
La razón trigonométrica Seno se calcula mediante la relación entre la longitud del cateto opuesto sobre la longitud de la hipotenusa:
La reazón trigonométrica Coseno se calcula mediante la relación entre la longitud del cateto adyacente y la hipotenusa:
La razón trigonométrica Tangente se calcula mediante la relación o división entre el cateto opuesto y el cateto adyacente:
Actividad 6: Establezca las razones Seno, Coseno y Tangente de alfa para cada uno de los triángulos del ejercicio anterior. Dibuje el triángulo de nuevo y al lado derecho escriba las razones.
Si dos triángulos rectos son semejantes, la razón Seno del ángulo congruente resulta equivalente, de igual manera para Coseno y Tangente.
Actividad 7. Calcular el valor de la hipotenusa o cateto opuesto, planteando la razón Seno.
7.1
7.2
Actividad 8: Establezca la razón Seno de alfa, obteniendo así la ecuación en forma de proporción y despeje la incógnita.
8.1
8.2
8.3
8.4 
8.5
Actividad 9: Establezca la razón coseno de alfa y despeje la incógnita.
9.1
9.2
9.3
9.4
Actividad 10: Solucione el triángulo rectángulo en términos del ángulo de referencia. Cuando tenga despejada la incógnita, haga uso de la calculadora para encontrar el valor de seno o coseno del ángulo pedido.
10.1
10.2
10.3
10.4
Actividad 11: Establezca la razón trigonométrica Tangente en los triángulos del punto 10, es necesario que dibuje el triángulo de nuevo.
Actividad 12: Resolver, construyendo el triángulo que es necesario par la mejor comprensión del problema.
12.1 Un poste de 10 metros de altura es amarrado al piso por medio de una cuerda que forma un ángulo de 45 ° con la horizontal. ¿Qué longitud tiene la cuerda?
12.2 La sombra de un edificio, en un momento del día, forma un ángulo de 20° con la horizontal. Si la sombra mide 50 metros, ¿qué altura tiene el edificio?
12.3 Una rampa tiene un altura de 50 cm, y forma un ángulo de 30° con la pared. ¿Qué ángulo forma con el piso y qué longitud de rampa tiene?
Fin del Taller.
No hay comentarios:
Publicar un comentario