Taller de nivelación Matemáticas Grado 11
---------------------------------------------------------------------
Fecha de entrega: Lunes 01 de agosto de 2011
Tema: Límites de funciones.
Criterios par la Presentación del trabajo: en hojas blancas (no cuadriculadas) tamaño carta u oficio, enunciado de la pregunta seguido de la respuesta que puede ir a lapicero o lápiz, pero la solución debe ir a lápiz. Puede escribir por ambas caras de la hoja. Por favor numerar las hojas al pie de página a mano para efectos de organización y buena presentación.
Actividad 1: Despejar X en cada caso.
a) x+2=3
b) x-2=3
c) 2x=8
d) 3x-1=13
e) x+a=c
f) x-a=c
g) ax+b=c
h) ax-b=c
i) (ax+1)/(1-ax)=1/1
j) 1/x + 1/2 = 3
Actividad 2: Graficar por medio de una tabulación, recomiendo de -5 a +1.
a) f(x)= 2x-1
b) f(x)=x²
c) f(x)=3x
d) f(x)= x / (x-9) En esta tenga en cuenta que el valor crítico es 9, tabule desde -4 a 13.
Actividad 3: Factorizar.
1) ax+bx+cx Solución x(a+b+c)
2) ax-bx
3) 4x+2
4) 3x+3y
5) 2x-2y
6) mn+n
7) ax²+bx
8) 4xy-8xy
9) x²-x³-x
10) x²-x³
11) 10x²-5x³
12) x(x-1) + y(x-1)
13) a(m+n) -b(m+n)
14) ax-bx +m(a-b)
15) y²-y +a(y-1)
16) y²-y +a(1-y)
17) ax-by +mx-my
18) x²+3x +2x +6........
19) y²+7y-2y-14
20) x²-5x+6 (convertir -5x en -3x -2x y factorizar por agrupación)
21) m²-7m-30.............
22) x²-1..........
23) m²-16...........
24) h²-144..............
25) 9k²-1 .........
26) 100-z²...........
27) (m)²-(m-a)²...............
28) x²+6x+9
29) y²-10y+25...............
30) a²-2ab+b²................
31) 4p²+4p+1........
32) 9y²+12y+4
Actividad 4: Realizar los siguientes productos, recuerde simplificar.
1) x(x+1)......................
2) x(x-1)............
3) -2x(x-3) + 4x( x+1).............
4) y(y-1) + y(y+1) - y²
5) (x+3) (x-2).............
6) (x-5)² ............
7) x²-1 + (x-1)².........................
8) (2a-3b)²
Actividad 5: Sumar.
1) 1/a + 2/a
2) 3/x + 4/x
3) m/2x + n/x Amplifique por 2 la segunda fracción para que sean homogéneas.
4) a/3x + b/6x Amplificar la primera por 2.
5) k/x² + k/x Amplifique la segunda por x, es decir que debe multiplicarla arriba y abajo por x.
6) r/s + r/s²
7) a/(x-1) + b /(x-1)²
8) x/(x-3) + y (x-3)
9) m/(x+2) + x/(x+2)²
10) m/(x+2) + x/(x²+2x+4).............. Factorice el trinomio de la segunda fracción.
11) a/x -b/(x²-x)
12) 1/x + 1/y
13) a/b + b/a
14) (x-1)/ x + x/(x-1) - (x+1)/(x-1)
Actividad 6: Cacular.
Nota: una expresión en función de x se denota por f(x), por ejemplo el área A de un cuadrado cuyo lado mide x, se calcula mediante la expresión de función:
A(x)=x²
Por ejemplo, A(3) = 3², en donde A(3)=9, que significa que el área de un cuadrado de lado 3 unidades es 9 unidades cuadradas.
En ocasiones es necesario calcular valores numéricos de la función, como el caso de x=3, entonces A(3)=9. También es necesario calcular valores literarales, es decir que la función toma expresiones algebraicas, como por ejemplo A(m+n) con A(x)=x² quedaría:
A(x)=x²
como x= m+n entonces quedaría
A(m+n)=(m+n) ²
o sea:
A(m+n)=m²+2mn+n²
Recuerde que (m+n)²= (m+n)(m+n) = mm+mn+nm+nn = m²+2mn+n²
1) Sea f(x)=2x-1, calcular f(-4)
2) Sea f(x)=4x-1, calcular f(m)
3) Sea f(x)=2x-1, calcular f(a+b)
4) Sea f(x)=2(x-1), calcular f(100)
4) Sea f(x)=2(x-1), calcular f(100)
5) Sea f(x)=3x+4, calcular f(x+h)
6) Sea f(x)=3x+4, calcular f(x+h)-(3x+4)
7) Sea f(x)=2x, calcular f(x+h)-f(x) Reemplace f(x) por 2x
8) Sea f(x)=5x-6, calcular f(x+h)-f(x) Reemplace f(x) por 5x-6
9) Sea f(x)=x², calcular f(x+h)-f(x) Reemplace f(x) por x²
10) Sea f(x)=x³, calcular f(x+h)-f(x)
11) Sea f(x)=1/x, calcular f(x+h)-f(x)
12) Sea f(x)=2x-34, calcular (f(x+h)-f(x)) / h
13) Sea f(x)=x²-3x+1, calcular (f(x+h)-f(x)) / h
Actividad 7: Simplificar.
1) (x²-x)/x
2) 3(x-1) / [(x+1)(x-1)]
3) (x²-9) / (x-3)
4) (x+3) /( x²-9)
5) (x²+7x+12) / (x+3)
6) (x²+3x-10) / (x²+6x+9)
7) (y²-4) / (y²+4y-12)
Actividad 8: Calcular el valor de la incógnita.
1) 2x=4
2) x²=16
3) 25=x
4) 3 x-1 =9
5) (x-1)²=16
6) 4x-2=64
7) √(x-1)=9
8) 2√x =8
9) 1-√x=10
10) |x| =5
11) |x-1| = 25
Actividad 9: Escribir el enunciado en notación de límite y calcular.
1) límite cuando x tiende a 3 de f(x)= 3x-2
2) límite cuando x tiende a 2 de f(x)= 1/x
3) límite cuando x tiende a 0 de f(x)= 1/x
4) límite cuando x tiende a -1 de f(x)= 1/(x+1)
5) límite cuando x tiende a infinito positivo de f(x)= 1/x
6) límite cuando x tiende a infinito negativo de f(x)= 1/x
7) límite cuando x tiende a infinito positivo de f(x)= 2x / (x-1)
8) límite cuando x tiende a infinito positivo de f(x)= (5x-3) / (2x-1)
9) límite cuando x tiende a 1de f(x)= (x-1) / (x²-1)
10) límite cuando x tiende a 1de f(x)= (x²+2x+1) / (x+1)
11) límite cuando x tiende a 3 de f(x)= (x-3) / (x²-9)
12) límite cuando x tiende a -3 de f(x)= (x-3) / (x²-9)
13) límite cuando x tiende a 2 de f(x)= (x²+3X-10) / (x²+5X-14)
14) límite cuando x tiende a 1 de f(x)= 1 / (1-√x)
15) límite cuando x tiende a 9 de f(x)= 1 / (3-√x) Debe racionalizar
16) límite cuando x tiende a 9 de f(x)= X / (X-√x) Racionalizar.
17) Límite cuando x-->0 de (x²+x) / (x²-x)
Actividad 10: Graficar las funciones 3, 7, 8, 9, 11, 14 y 17 de la actividad 9. Receurde trazar asíntotas y unicar puntos de discontinuidad. También recuerde indicar el límite a los valores críticos, diga si exite o no y de existir, debe calcularlo.
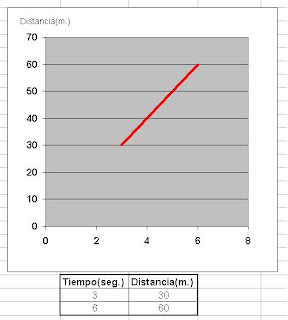





 Significa que las dos carreteras están separadas 90 metros.
Significa que las dos carreteras están separadas 90 metros.
































