COMASACA, Matemáticas, Grado 9, Periodo II, Tema: Sistemas de Ecuaciones Lineales.

En el siguiente texto tendrás que completar algunas oraciones y operaciones a manera de ejericitación en el tema.

RECORDEMOS LO QUE VENÍAMOS HACIENDO.

Hasta el momento, hemos visto como dos cantidades o magnitudes varían, una respecto de la otra. Por ejemplo el costo "C" de un plan de teléfonía celular, que está en función del tiempo "t" consumido y del cargo básico. La expresión C=250t+10000 como ecuación de costo para la empresa A, nos indicaba que C dependía de t, por ejemplo si t=10 minutos, el costo era de __________________. La imagen 1 muestra la manera como varía el costo en función del tiempo.

Las magnitudes que variaban fueron estudiadas en la función lineal, sin adicionar otra condición. Pero cuando ya se hablaba de una segunda situación relacionada con la primera, por ejemplo otra empresa B cuya formula era C= 300t+8000, se formulaban interrogantes cuya respuesta requería de analizarlas en conjunto. Como pudiste calcular, para un consumo de 10 minutos la empresa A cobra $12.500 y en la empresa B sería de $11.000. Al diligenciar la tabla de valores para las dos empresas, ¿para cuál valor de t, ambas empresas cobran lo mismo? Al Diliegenciar la tabla de valores de la Figura 1. nos damos cuenta que

_________________________________________________________________

_________________________________________________________________

Estas situaciones de linealidad que deben ser analizadas en conjunto, reciben el nombre de problemas de sistemas lineales. Cuando se pretende resolver las ecuaciones para depejar incógnitas referidas a sus magnitudes, reciben el nombre de Sistemas de Ecuaciones Lineales (SEL).

El SEL para el problema del consumo a celular de las mpresas A y B sería:

CA=250t+10000 y CB= 300t+8000.

Como pudiste ver en la tabla, el consumo de A y el Consumo de B son iguales en valor cuando t=40 ¿por qué? Ver imagen 2.

Para responder a este interrogante, es necesario igualar CA con CB, pues preguntan el valor de t para el cual estas dos cantidades son equivalentes.

CA=CB

250t+10000=300t+8000

10000-8000= 300t-250t

2000=50t

2000/50=t

40=t

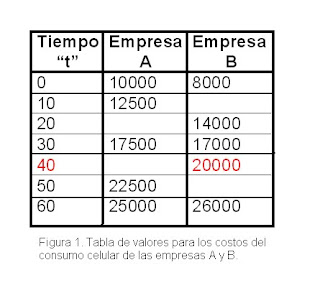
Indica entonces que para un consumo de 40 minutos ambas empresas cobran el mismo valor. Quiere decir que antes de los 40 minutos es mejor la empresa ___, a los 40 minutos ______________ de las empesas es mejor y después de los 40 minutos es mejor la empresa _____.

Como pudimos ver, las ecuaciones de las empresas A y B forman un s_________de e____________s.

Como estudiante, debes adquirir habiliades para resolver situaciones problema que requieren de plantear un sistemas de ecuaciones, resolverlo e interpretar la solución. Para esto, el grupo de maestros del COMASACA, han propuesto el siguiente indicador de desempeño: comprendo enunciados de problemas matemáticos que involucren funciones, sistemas de ecuaciones y medidas de precisión para poliedros. Lo más importante de esto está en la potenciación de habiliades de pensamiento superior, en cuanto a que se debe "comprender", acto mental necesario en cualquier actividad humana.

Veamos la siguiente situación: Diana recibe un paquete de 165 unidades, entre bananas y bombones, para repartirlo a 111 infantes que asisten a la fiesta de su hija. La persona que le vendió el paquete le dijo que podía repartir, sin que sobrarán, a cada niño un par de bananas y a cada niña un bombón. ¿Cuántos niños y niñas habían en la fiesta?

Para resolver un problema de SEL, es necesario llevar a supuestos valores la situación, para comprenderla desde las operaciones aritméticas que varían, para luego representar estas cantidades desde letras o variables.

Supongamos que hay 10 niñas y 8 niños, es decir 18 infantes, para los cuales las niñas reciben 10 bombones y los niños reciben 16 bananas, que dan un total de 26 uniades de dulce, situación que no coincide con la del problema. Pensemos ahora que hay 100 niñas y 11 niños, para los cuales hay 100 bombones y 22 bananas, que dan un total de 122 unidaes, que tampoco cumple con las condiciones.

Este proceso se denomina de ensayo y error (e/e), que facilita la comprensión del problema en la medida que se pueda representar los sucesos repetitivos por medio de variables. Los diferentes valores de la situación dada, se mmuestran en la siguiente tabla:

h	m	Bananas	Bombones	Bananas+bombones
1	110	2	110	112
2	109	4	109	113
3	108	6	108	114
4	107	8	107	115
5	106	10	106	116
6	105	12	105	117
7	104	14	104	118
8	103	16	103	119
9	102	18	102	120
10	101	20	101	121
11	100	22	100	122
12	99	24	99	123
13	98	26	98	124
14	97	28	97	125
15	96	30	96	126
16	95	32	95	127
17	94	34	94	128
18	93	36	93	129
19	92	38	92	130
20	91	40	91	131
21	90	42	90	132
22	89	44	89	133
23	88	46	88	134
24	87	48	87	135
25	86	50	86	136
26	85	52	85	137
27	84	54	84	138
28	83	56	83	139
29	82	58	82	140
30	81	60	81	141
31	80	62	80	142
32	79	64	79	143
33	78	66	78	144
34	77	68	77	145
35	76	70	76	146
36	75	72	75	147
37	74	74	74	148
38	73	76	73	149
39	72	78	72	150
40	71	80	71	151
41	70	82	70	152
42	69	84	69	153
43	68	86	68	154
44	67	88	67	155
45	66	90	66	156
46	65	92	65	157
47	64	94	64	158
48	63	96	63	159
49	62	98	62	160
50	61	100	61	161
51	60	102	60	162
52	59	104	59	163
53	58	106	58	164
54	57	108	57	165
55	56	110	56	166
56	55	112	55	167
57	54	114	54	168
58	53	116	53	169
59	52	118	52	170
60	51	120	51	171
61	50	122	50	172
62	49	124	49	173
63	48	126	48	174
64	47	128	47	175
65	46	130	46	176
66	45	132	45	177
67	44	134	44	178
68	43	136	43	179
69	42	138	42	180
70	41	140	41	181
71	40	142	40	182
72	39	144	39	183
73	38	146	38	184
74	37	148	37	185
75	36	150	36	186
76	35	152	35	187
77	34	154	34	188
78	33	156	33	189
79	32	158	32	190
80	31	160	31	191
81	30	162	30	192
82	29	164	29	193
83	28	166	28	194
84	27	168	27	195
85	26	170	26	196
86	25	172	25	197
87	24	174	24	198
88	23	176	23	199
89	22	178	22	200
90	21	180	21	201
91	20	182	20	202
92	19	184	19	203
93	18	186	18	204
94	17	188	17	205
95	16	190	16	206
96	15	192	15	207
97	14	194	14	208
98	13	196	13	209
99	12	198	12	210
100	11	200	11	211
101	10	202	10	212
102	9	204	9	213
103	8	206	8	214
104	7	208	7	215
105	6	210	6	216
106	5	212	5	217
107	4	214	4	218
108	3	216	3	219
109	2	218	2	220
110	1	220	1	221

En rojo aparece la única situación que cumple las dos condiciones. Nótese que existen 110 posibilidades en el E/E, situación que tomaría mucho tiempo, pero que es esencial a la hora de comprender la dinámica en la solución del problema.

Supongamos ahora que hay "h" niños y "m" niñas, donde h+m=111 y que a cada niño se le dan dos bananas, donde el total de bananas es 2h, ya para las mujeres el total de bombones es m, de donde 2h+m=165 unidades. Obtenemos entonces un SEL´s que se escribe así:

¿Cómo solucionarlo?

Para solucionar este sistema de ecuaciones hay que acudir a un método. Existen varios métodos para la solución de un SEL´s: eliminación, sustitución, igualación y determinantes.

Método de Eliminación o Reducción.

Consiste en eliminar una de las incógnitas haciendo uso de la propiedad de la adición de la igualdad: al sumar los miembros de dos igualdades, la igualdad permanece. Más claro, si 5=5 y 4=4, entonces 5+4=5+4, que es verdadero. Además del uso del inverso aditivo que afirma que todo número real tiene un inverso aditivo y que al sumar un número con su inverso aditivo se obtiene cero (0), por ejemplo 4 sumado con -4 da 0.

Busquemos que al sumar ambas igualdades se cancele una de las incógnitas, en este caso la m:

Lo que se hizo fue multiplicar la primera ecuación por -1 (propiedad uniforme), de tal manera que la m quede con coeficientes inversos aditivos ( +1 y -1 son inversos aditivos ya que sumados dan 0).

Al sumar la primera ecuación con la segunda ecuación, se obtiene:

de donde

1h + 0m = 54

h=54

La cantidad de hombres es de 54 y la de mujeres es:

54+ m = 111

m= 111-54

m= 57

Por consiguiente hay 57 bombones y 2(54) = 108 bananas para 57 mujeres y 54 hombres.

Es necesario identificar que se repiten unos pasos en éste método, que son:

PASOS SUGERIDOS EN EL MÉTODO DE ELIMINACIÓN

I. Se deben escribir las ecuaciones de la forma ax+by=c. Por ejemplo, si una de las ecuaciones aparece como 2(3x-1) =3(2y-5), se deben realizar las operaciones necesarias así:

2(3x-1) =3(2y-5)
6x-2=6y-15
6x-6y=-15+2
6x-6y=-13

II. Se debe seleccionar la incógnita a eliminar, realizar las tranformaciones necesarias para que ésta quede en ambas ecuaciones con coeficientes que sean inversos aditivos. Por ejemplo para

(1) 2x-3y=4
(2) 4x+6y=10

Si se quiere eliminar la y, se debe multiplicar la primera ecuación por 2:

(1) 2(2x-3y)= 2(4)
(2) 4x+6y=10

Quedando:

(3) 4x-6y= 8
(2) 4x+6y=10

Es evidente que al sumar ambas ecuaciones, la incógnita y se cancela. Nótese que la ecuación (1) cambió por (3) ya que se amplificó por 2, de tal manera que cambia y es necesario también cambiar su etiqueta.

III. Sumar las ecuaciones y eliminar la incógnita seleccionada:

(3) 4x-6y= 8
(2) 4x+6y=10
---------- ------
4x+4x-6y+6y=18
8x+0y=18
8x=18
x=18/8
x=9/4

El verdadero desafío consiste en identificar los valores por los cuales debe amplificar o simplificar las ecuaciones para que la incógnita seleccionada se cancele.

IV. Reemplazar el valor encontrado en cualquierqa de las ecuaciones originales para despejar la otra incógnita y dar solución al sistema mediante una pareja ordenada (x,y).

Reemplazando 9/4 como valor de x en la primera ecuación, resulta:

2x-3y=4

2(9/4)-3y=4
18/4-3y=4
9/2-3y=4
9/2-4=3y
9/2-8/2=3y
1/2=3y
1/6=y

V. Verificar si son correctos los valores encontrados: para esto cada uno de los valores se reemplazan en ambas ecuaciones de tal manera que si son correctas, se obtienen dos igualdades.

(1) 2(9/4)-3(1/6)=4
(2) 4(9/4)+6(1/6)=10



Solución: (9/4 , 1/6)

http://thales.cica.es/rd/Recursos/rd97/Problemas/09-02-p-SisEcuProblemas.html