En el siguiente texto tendrás que completar algunas oraciones y operaciones a manera de ejericitación en el tema.
RECORDEMOS LO QUE VENÍAMOS HACIENDO.
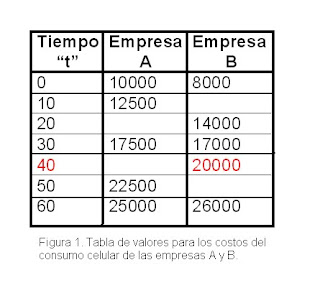
Hasta el momento, hemos visto como dos cantidades o magnitudes varían, una respecto de la otra. Por ejemplo el costo "C" de un plan de teléfonía celular, que está en función del tiempo "t" consumido y del cargo básico. La expresión C=250t+10000 como ecuación de costo para la empresa A, nos indicaba que C dependía de t, por ejemplo si t=10 minutos, el costo era de __________________. La imagen 1 muestra la manera como varía el costo en función del tiempo.
Las magnitudes que variaban fueron estudiadas en la función lineal, sin adicionar otra condición. Pero cuando ya se hablaba de una segunda situación relacionada con la primera, por ejemplo otra empresa B cuya formula era C= 300t+8000, se formulaban interrogantes cuya respuesta requería de analizarlas en conjunto. Como pudiste calcular, para un consumo de 10 minutos la empresa A cobra $12.500 y en la empresa B sería de $11.000. Al diligenciar la tabla de valores para las dos empresas, ¿para cuál valor de t, ambas empresas cobran lo mismo? Al Diliegenciar la tabla de valores de la Figura 1. nos damos cuenta que
_________________________________________________________________
_________________________________________________________________
Estas situaciones de linealidad que deben ser analizadas en conjunto, reciben el nombre de problemas de sistemas lineales. Cuando se pretende resolver las ecuaciones para depejar incógnitas referidas a sus magnitudes, reciben el nombre de Sistemas de Ecuaciones Lineales (SEL).
El SEL para el problema del consumo a celular de las mpresas A y B sería:
CA=250t+10000 y CB= 300t+8000.
Como pudiste ver en la tabla, el consumo de A y el Consumo de B son iguales en valor cuando t=40 ¿por qué? Ver imagen 2.
Para responder a este interrogante, es necesario igualar CA con CB, pues preguntan el valor de t para el cual estas dos cantidades son equivalentes.
CA=CB
250t+10000=300t+8000
10000-8000= 300t-250t
2000=50t
2000/50=t
40=t
Indica entonces que para un consumo de 40 minutos ambas empresas cobran el mismo valor. Quiere decir que antes de los 40 minutos es mejor la empresa ___, a los 40 minutos ______________ de las empesas es mejor y después de los 40 minutos es mejor la empresa _____.
Como pudimos ver, las ecuaciones de las empresas A y B forman un s_________de e____________s.
Como estudiante, debes adquirir habiliades para resolver situaciones problema que requieren de plantear un sistemas de ecuaciones, resolverlo e interpretar la solución. Para esto, el grupo de maestros del COMASACA, han propuesto el siguiente indicador de desempeño: comprendo enunciados de problemas matemáticos que involucren funciones, sistemas de ecuaciones y medidas de precisión para poliedros. Lo más importante de esto está en la potenciación de habiliades de pensamiento superior, en cuanto a que se debe "comprender", acto mental necesario en cualquier actividad humana.
Veamos la siguiente situación: Diana recibe un paquete de 165 unidades, entre bananas y bombones, para repartirlo a 111 infantes que asisten a la fiesta de su hija. La persona que le vendió el paquete le dijo que podía repartir, sin que sobrarán, a cada niño un par de bananas y a cada niña un bombón. ¿Cuántos niños y niñas habían en la fiesta?
Para resolver un problema de SEL, es necesario llevar a supuestos valores la situación, para comprenderla desde las operaciones aritméticas que varían, para luego representar estas cantidades desde letras o variables.
Supongamos que hay 10 niñas y 8 niños, es decir 18 infantes, para los cuales las niñas reciben 10 bombones y los niños reciben 16 bananas, que dan un total de 26 uniades de dulce, situación que no coincide con la del problema. Pensemos ahora que hay 100 niñas y 11 niños, para los cuales hay 100 bombones y 22 bananas, que dan un total de 122 unidaes, que tampoco cumple con las condiciones.
Este proceso se denomina de ensayo y error (e/e), que facilita la comprensión del problema en la medida que se pueda representar los sucesos repetitivos por medio de variables. Los diferentes valores de la situación dada, se mmuestran en la siguiente tabla:
| h | m | Bananas | Bombones | Bananas+bombones |
| 1 | 110 | 2 | 110 | 112 |
| 2 | 109 | 4 | 109 | 113 |
| 3 | 108 | 6 | 108 | 114 |
| 4 | 107 | 8 | 107 | 115 |
| 5 | 106 | 10 | 106 | 116 |
| 6 | 105 | 12 | 105 | 117 |
| 7 | 104 | 14 | 104 | 118 |
| 8 | 103 | 16 | 103 | 119 |
| 9 | 102 | 18 | 102 | 120 |
| 10 | 101 | 20 | 101 | 121 |
| 11 | 100 | 22 | 100 | 122 |
| 12 | 99 | 24 | 99 | 123 |
| 13 | 98 | 26 | 98 | 124 |
| 14 | 97 | 28 | 97 | 125 |
| 15 | 96 | 30 | 96 | 126 |
| 16 | 95 | 32 | 95 | 127 |
| 17 | 94 | 34 | 94 | 128 |
| 18 | 93 | 36 | 93 | 129 |
| 19 | 92 | 38 | 92 | 130 |
| 20 | 91 | 40 | 91 | 131 |
| 21 | 90 | 42 | 90 | 132 |
| 22 | 89 | 44 | 89 | 133 |
| 23 | 88 | 46 | 88 | 134 |
| 24 | 87 | 48 | 87 | 135 |
| 25 | 86 | 50 | 86 | 136 |
| 26 | 85 | 52 | 85 | 137 |
| 27 | 84 | 54 | 84 | 138 |
| 28 | 83 | 56 | 83 | 139 |
| 29 | 82 | 58 | 82 | 140 |
| 30 | 81 | 60 | 81 | 141 |
| 31 | 80 | 62 | 80 | 142 |
| 32 | 79 | 64 | 79 | 143 |
| 33 | 78 | 66 | 78 | 144 |
| 34 | 77 | 68 | 77 | 145 |
| 35 | 76 | 70 | 76 | 146 |
| 36 | 75 | 72 | 75 | 147 |
| 37 | 74 | 74 | 74 | 148 |
| 38 | 73 | 76 | 73 | 149 |
| 39 | 72 | 78 | 72 | 150 |
| 40 | 71 | 80 | 71 | 151 |
| 41 | 70 | 82 | 70 | 152 |
| 42 | 69 | 84 | 69 | 153 |
| 43 | 68 | 86 | 68 | 154 |
| 44 | 67 | 88 | 67 | 155 |
| 45 | 66 | 90 | 66 | 156 |
| 46 | 65 | 92 | 65 | 157 |
| 47 | 64 | 94 | 64 | 158 |
| 48 | 63 | 96 | 63 | 159 |
| 49 | 62 | 98 | 62 | 160 |
| 50 | 61 | 100 | 61 | 161 |
| 51 | 60 | 102 | 60 | 162 |
| 52 | 59 | 104 | 59 | 163 |
| 53 | 58 | 106 | 58 | 164 |
| 54 | 57 | 108 | 57 | 165 |
| 55 | 56 | 110 | 56 | 166 |
| 56 | 55 | 112 | 55 | 167 |
| 57 | 54 | 114 | 54 | 168 |
| 58 | 53 | 116 | 53 | 169 |
| 59 | 52 | 118 | 52 | 170 |
| 60 | 51 | 120 | 51 | 171 |
| 61 | 50 | 122 | 50 | 172 |
| 62 | 49 | 124 | 49 | 173 |
| 63 | 48 | 126 | 48 | 174 |
| 64 | 47 | 128 | 47 | 175 |
| 65 | 46 | 130 | 46 | 176 |
| 66 | 45 | 132 | 45 | 177 |
| 67 | 44 | 134 | 44 | 178 |
| 68 | 43 | 136 | 43 | 179 |
| 69 | 42 | 138 | 42 | 180 |
| 70 | 41 | 140 | 41 | 181 |
| 71 | 40 | 142 | 40 | 182 |
| 72 | 39 | 144 | 39 | 183 |
| 73 | 38 | 146 | 38 | 184 |
| 74 | 37 | 148 | 37 | 185 |
| 75 | 36 | 150 | 36 | 186 |
| 76 | 35 | 152 | 35 | 187 |
| 77 | 34 | 154 | 34 | 188 |
| 78 | 33 | 156 | 33 | 189 |
| 79 | 32 | 158 | 32 | 190 |
| 80 | 31 | 160 | 31 | 191 |
| 81 | 30 | 162 | 30 | 192 |
| 82 | 29 | 164 | 29 | 193 |
| 83 | 28 | 166 | 28 | 194 |
| 84 | 27 | 168 | 27 | 195 |
| 85 | 26 | 170 | 26 | 196 |
| 86 | 25 | 172 | 25 | 197 |
| 87 | 24 | 174 | 24 | 198 |
| 88 | 23 | 176 | 23 | 199 |
| 89 | 22 | 178 | 22 | 200 |
| 90 | 21 | 180 | 21 | 201 |
| 91 | 20 | 182 | 20 | 202 |
| 92 | 19 | 184 | 19 | 203 |
| 93 | 18 | 186 | 18 | 204 |
| 94 | 17 | 188 | 17 | 205 |
| 95 | 16 | 190 | 16 | 206 |
| 96 | 15 | 192 | 15 | 207 |
| 97 | 14 | 194 | 14 | 208 |
| 98 | 13 | 196 | 13 | 209 |
| 99 | 12 | 198 | 12 | 210 |
| 100 | 11 | 200 | 11 | 211 |
| 101 | 10 | 202 | 10 | 212 |
| 102 | 9 | 204 | 9 | 213 |
| 103 | 8 | 206 | 8 | 214 |
| 104 | 7 | 208 | 7 | 215 |
| 105 | 6 | 210 | 6 | 216 |
| 106 | 5 | 212 | 5 | 217 |
| 107 | 4 | 214 | 4 | 218 |
| 108 | 3 | 216 | 3 | 219 |
| 109 | 2 | 218 | 2 | 220 |
| 110 | 1 | 220 | 1 | 221 |
En rojo aparece la única situación que cumple las dos condiciones. Nótese que existen 110 posibilidades en el E/E, situación que tomaría mucho tiempo, pero que es esencial a la hora de comprender la dinámica en la solución del problema.
Supongamos ahora que hay "h" niños y "m" niñas, donde h+m=111 y que a cada niño se le dan dos bananas, donde el total de bananas es 2h, ya para las mujeres el total de bombones es m, de donde 2h+m=165 unidades. Obtenemos entonces un SEL´s que se escribe así:
¿Cómo solucionarlo?
Para solucionar este sistema de ecuaciones hay que acudir a un método. Existen varios métodos para la solución de un SEL´s: eliminación, sustitución, igualación y determinantes.
Método de Eliminación o Reducción.
Consiste en eliminar una de las incógnitas haciendo uso de la propiedad de la adición de la igualdad: al sumar los miembros de dos igualdades, la igualdad permanece. Más claro, si 5=5 y 4=4, entonces 5+4=5+4, que es verdadero. Además del uso del inverso aditivo que afirma que todo número real tiene un inverso aditivo y que al sumar un número con su inverso aditivo se obtiene cero (0), por ejemplo 4 sumado con -4 da 0.
Busquemos que al sumar ambas igualdades se cancele una de las incógnitas, en este caso la m:
Lo que se hizo fue multiplicar la primera ecuación por -1 (propiedad uniforme), de tal manera que la m quede con coeficientes inversos aditivos ( +1 y -1 son inversos aditivos ya que sumados dan 0).
Al sumar la primera ecuación con la segunda ecuación, se obtiene:
de donde
1h + 0m = 54
h=54
La cantidad de hombres es de 54 y la de mujeres es:
54+ m = 111
m= 111-54
m= 57
Por consiguiente hay 57 bombones y 2(54) = 108 bananas para 57 mujeres y 54 hombres.
Es necesario identificar que se repiten unos pasos en éste método, que son:
PASOS SUGERIDOS EN EL MÉTODO DE ELIMINACIÓN
I. Se deben escribir las ecuaciones de la forma ax+by=c. Por ejemplo, si una de las ecuaciones aparece como 2(3x-1) =3(2y-5), se deben realizar las operaciones necesarias así:
2(3x-1) =3(2y-5)
6x-2=6y-15
6x-6y=-15+2
6x-6y=-13
II. Se debe seleccionar la incógnita a eliminar, realizar las tranformaciones necesarias para que ésta quede en ambas ecuaciones con coeficientes que sean inversos aditivos. Por ejemplo para
(1) 2x-3y=4
(2) 4x+6y=10
Si se quiere eliminar la y, se debe multiplicar la primera ecuación por 2:
(1) 2(2x-3y)= 2(4)
(2) 4x+6y=10
Quedando:
(3) 4x-6y= 8
(2) 4x+6y=10
Es evidente que al sumar ambas ecuaciones, la incógnita y se cancela. Nótese que la ecuación (1) cambió por (3) ya que se amplificó por 2, de tal manera que cambia y es necesario también cambiar su etiqueta.
III. Sumar las ecuaciones y eliminar la incógnita seleccionada:
(3) 4x-6y= 8
(2) 4x+6y=10
---------- ------
4x+4x
-6y+
6y=18
8x+
0y=18
8x=18
x=18/8
x=9/4
El verdadero desafío consiste en identificar los valores por los cuales debe amplificar o simplificar las ecuaciones para que la incógnita seleccionada se cancele.
IV. Reemplazar el valor encontrado en cualquierqa de las ecuaciones originales para despejar la otra incógnita y dar solución al sistema mediante una pareja ordenada (x,y).
Reemplazando 9/4 como valor de x en la primera ecuación, resulta:
2x-3y=4
2(9/4)-3y=4
18/4-3y=4
9/2-3y=4
9/2-4=3y
9/2-8/2=3y
1/2=3y
1/6=y
V. Verificar si son correctos los valores encontrados: para esto cada uno de los valores se reemplazan en ambas ecuaciones de tal manera que si son correctas, se obtienen dos igualdades.
(1) 2(
9/4)-3(
1/6)=4
(2) 4(
9/4)+6(
1/6)=10
Solución: (9/4 , 1/6)
