COMASACA 9-1 y 9-2 Taller #2 de Recuperación: matemáticas, geometría y estadística.

La experiencia en cuanto a la entrega de los trabajos escritos del taller de refuerzo #1 sirvió para identificar algunas características de los grados novenos del COMASACA, entre ellas la actitud, en la mayoría, de entregar trabajos estéticamente mal presentados. La hoja inicial en colores, mal distribuida, con casos ortográficos y hasta sin hoja de presentación. Algunos atribuyeron esto al poco tiempo para realizarlo, pero esta hoja no tomaba tanto en construirla. Algunos estudiantes presentaron primero las preguntas y luego las respuestas, otros respondieron sin las justificaciones y procesos pertinentes y otros escribieron la pregunta sin respuesta y sin proceso., ¿qué perseguían con esto? Estas situaciones hay que remediarlas de inmediato mediante la toma de conciencia de la importancia de llevar a cabo este tipo de trabajo. No es un secreto que para aprender matemáticas hay que practicar y repetir procesos mediante la aplicación de condiciones y criterios que la rigen; para esto el estudiante debe habituarse a delegar tiempos frecuentes para afianzar en matemáticas.

Cabe mencionar que enalgunos estudiantes se evidencia el gusto por las matemáticas, en otros no tanto y a la minoría parece no llamarle la atención. Es necesario recordar que el propósito esencial de aprenderla está en desarrollar el pensamiento lógico, necesario en cualquier situación que se presente en el transcurso de la vida. Analizar situaciones, construir opciones, seleccionar alternativas, evaluar un camino a tomar, prevenir eventos, ser consecuentes, entre otra gran cantidad de operaciones mentales que se llevan a cabo en el diario vivir y que se potencian desde las diferentes áreas de conocimiento, entre ellas las matemáticas.

Los talleres aquí registrados estan dosificados y estrucurados de tal manera que el estudiante se sienta como si estuviera con el profesor al lado, es dejar implícito la comunicación dialógica a medida que va solucionándolos, claro está en la medida de lo posible, pues no se pretende obviar el roll del maestro docente en clase. Se espera que el estudiante otorgue tiempo a esta actividad, las dudas me las haga llegar al correo electrónico y termine satisfactoriamente lo propuesto.

Taller de Matemáticas.

Tema: Conceptos básicos de Función y Función lineal.

1. Sea f una correspondencia de A en B definida como F={(x,y), x ϵ A ^ y ϵ B/ y = (3-x)(x-1) }, hallar las parejas que pertenecen a F si A={-1,0,1,2,3} y B={-10, -9,...,0 , 1}, luego indique por qué no es función.

2. Indicar cuáles de las siguientes asignaciones son funciones de A en B con A={1,2,3}, y B={1,2,3} y calsifíquelas. Justificar la respuesta

a. {(1,1), (2,1), (3,1)}
b.{(2,1), (2,2)}
c.{(1,1), (1,2), (2,3), (3,3)}
d.{(1,1), (1,2), (1,3)}
e.{(1,3), (2,3), (3,3)}
f.{(1,1), (2,2), (3,3)}

3. Escribir el dominio y rango de la función g, con

a. G={(2,4),(3,2),(1,0)}
b. G={(5,4),(5,2),(5,0)}
c. G={(1,1),(2,2),(3,2)}
d. G={(0,0),(3,2),(1,0),(2,4),(3,4),(1,6)}}

4. Explique por qué la función f definida de A-->B, con A={-1, 0, 1} y B={156, 100, 44, -12 } tal que f(x)=100-56x, no es sobreyectiva.

5. Verifique sie en la función f de reales en reales (se escribe R->R), con f(x)= (x+1)(x-1) se verifica para cualquier par de números a, b en el dominio, f(a)≠f(b) cuando a=b?.

6. Sea f una función de R->R con f(x)= 5/(x-3), explique por qué no es función. Nota: pregúntese si f(3) existe, es decir si el 3 del dominio tiene imagen en el codominio y guíese por la definición de función, si es necesario grafique.

7. Sea X={1,2,3,4,5}, hallar el rango de la función f(x)=5x-4, de codominio Y={-5,-4,...,12,13,14,15}.

8. Represente gráficamente la función y=10-5x, mediante una tabulación con valores para x entre -5 y 5.

9. Despejar y en las siguientes ecuaciones: Nota: recuerde efectuar correctamente expresiones como (x+c)² que equivalen a x²+2xc+c².

a. 3x+2y=5
b. 5x-12y=5
c. 12x-30y=12
d. 35a+2by=6
e. 3(x-10) + 4(15-y)=0
f. x(x-11)+3y= x(x+12)+5y-100
g. 5/x +y=3-2y
h. 4x=1/(5y-10)
i. (3x-2)²+y = 3x(3x-10)
j. (x-1)²+(y-2)² = (x+3)² + (y+5)²

10. Indique cuáles de las ecuaciones del problema anterior, representan líneas rectas. Aplique el flujograma visto en clase para clasificar funciones lineales.

11. Represente en el plano cartesiano algunas parejas (x,y) tales que la suma de las abscisas con las ordenadas sea 5.

12. Represente en el plano cartesiano algunas parejas (x,y) tales que la diferencia entre las abscisas con las ordenadas sea 2.

13. Represente en el plano las parejas (x,y) tales que x por y sea equivalente a 24. (algebraicamente xy= 24) ¿Qué concluyes del lugar geométrico de puntos obtenidos? ¿Es una línea recta en el plano? Explica. Nota: recuerde también tabular con valores negativos.

14. Una persona recorre 4 km en 12 minutos, es de esperarse que el doble de esta distancia la haga en 24 minutos y que el triple la haga en 36 minutos. Represente esta situación el plano cartesiano donde la distancia esté en función del tiempo.

15. Una persona recorre 4 km en 12 minutos, pero el doble de esta distancia no la hace en 24 sino en 15 minutos. ¿En cuánto tiempo recorrerá 12 km? Graficar, hallar la pendiente de la recta, reemplazar en la ecuación punto pendiente y escribir la ecuación que relaciona la distancia x con el tiempo t que tarda en recorrerla.

16. Hallar la pendiente de la recta que pasa por los puntos:

a. (2,3) y (5,-4)

b. (0,1) y (-2,4)

c. (-1,-2) y (-1, -5) tengamucho cuidado con el cálculo de la pendiente.

d. (a,b) y (b,a)

e. (1,d) y (d,1)

f. (h,hj) y (1, j) Recuerde simplificar la pendiente.

17. Por cada 20 cm de altura de una rampa, se avanzan 35 cm. ¿Qué altura h tiene una rampa en la cual se han avanzado 200 metros hasta su final? Plantear ecuación y resolverla para h.

18. Una empresa de celulares calcula que el pago P (en pesos) de un usuario que consume t minutos está dado por a ecuación p=500(120+t):

a. ¿Cuánto le cobran por t=0 minutos? ¿Este valor qué representa en la recta?
b. ¿Calcule la pendiente entre t=20 minutos y t= 30 minutos. ¿Qué representa este valor en la recta y en el contexto del problema?
c. Calcular t para un consumo p=$14.000
d. Represente p en función de t.

19. Dos rectas en el plano son paralelas si tienen pendientes equivalentes. Indique cuáles de las siguientes ecuaciones de recta, al representarlas en el plano, son paralelas a 3x-4y= 12

a. y=2x-3
b. y=0.75x-4
c. y=6/8 x-1
d. y=3/2 x+4

20. Dos vehículos parten de manera simultánea y en sentidos opuestos, desde dos ciudades distantes 100 km y en línea recta. El primero recorre una distancia x en km en un tiempo t en horas, de acuerdo a la ecuación x=4t+2 y el segundo de acuerdo a la ecuación x=2t+6.

a. ¿Cuánto tiempo tardan los vehículos en llegar a la ciudad opuesta?
b.¿Cuál de los dos llega primero?
c. Cuando llega el primer vehículo a su ciudad opuesta, ¿cuánto le falta al otro para llegar?
d. En el viaje, ¿en que momento (tiempo) se encuentran?
e. Represente los dos movimientos en el plano de tal manera que x esté en función de t, ¿qué concluyes?

Taller de Geometría.

1. En los triángulos ABC y PQR que se muestran en la figura, se puede afirmar que el ángulo A tiene como ángulo correspondiente el ángulo:

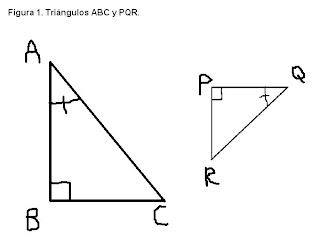
a. P porque el ángulo A es de 90º

b. Q porque así lo indica la figura según el símbolo.

c. R porque es el que hace falta.







2. Según la figura 1, el ángulo C es congruente (tiene la misma medida) que el ángulo:

a. R, porque los ángulos A y Q son también congruentes.

b. R, porque los ángulos A y Q son también congruentes lo mismo que B y P que equivalen a 90º.

c. R, porque los triángulos están en distinta posición.


3. Según la figura 1, el lado correspondiente al lado BC es PR porque:

___________________________________________________________

___________________________________________________________


4. Según la figura 1, es correcto afirmar que AB/PQ es equivalente a:

a. AC/PR

b. AB/QR

c. BC/RQ

5. La figura 2 muestra los triángulos ABC y PQR con AB=20, BC=15 y PQ=10. De acuerdo con las indicaciones en los ángulos, se puede establecer que son semejantes por el criterio AAA, en donde AB/PQ=AC/QR=BC/PR = K, donde K es la constante de proporcionalidad. El valor de K es:

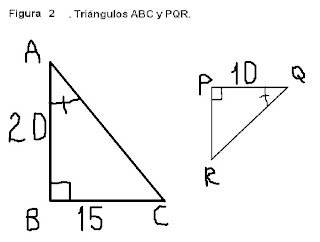
a. 1

b. 2

c. 3

d. 4






6. Según la figura 2, el valor de la longitud del segmento PR es: (Recuerde mostrar el proceso de planteamiento y solución)

a. 7.1

b. 7.3

c. 7.5

d. 7.8


7. Según la figura 2, es correcto afirmar que:

a. Los triángulos son congruentes.
b. Los triángulos son semejantes y de igual tamaño
c. Los triángulos son semejantes ya que el pequeño es la mitad del grande.
d. Los triángulos son semejantes ya que el grande es el doble del pequeño.

8. Como los triángulos de la figura #2 son rectos, se puede llamar catetos a los lados AB y BC del grande y PQ y PR del pequeño. Si se sabe que el área de un triángulo recto es equivalente al semiproducto (producto que se divide en dos partes iguales) de las longitudes de sus catetos, por ejemplo para el triángulo grande su área (área inicial Ai) es:

Ai = 20(10)/2
A=200/2
A=100.
y para el triángulo pqueño su área final Af es:
Af= PQ (PR)/2
Af=10(PR)/2

Al calcular el valor de PR y hallar Af, se puede afirmar que:

a. Af=2Ai
b. Af es mayor que Ai
c. Af es menor que Ai
d. Af=4Ai

9. Del problema anterior se puede generalizar afirmando que si la constante de proporcionalidad de dos triángulos rectos es k, la razón entre sus áreas es:

a. k

b. nk

c. 1/k

d. k²

10. Cuando se nombran los ángulos de un triángulo se acostumbra a mencionar los tres vértices que lo conforman, dejando en el centro el vértice que forma el ángulo. Por ejemplo el ángulo marcado como 1 (en la figura de abajo) tiene como vértice a M, pero se nombra como NMO, dejando a M en el centro. El ángulo O se puede nombrar como MON ó POQ. Cabe resaltar que estos ángulos son opuestos por el vértice O, de donde se deduce que:

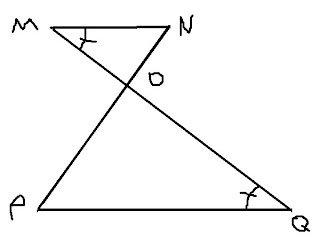
a. Los ángulos MON y POQ difieren en medida.


b. Los ángulos MON y POQ son congruentes por se opuestos por el vértice O.


c. Lo ángulos MON y POQ son semejantes.





11. De acuerdo a la figura del problema 10, el ángulo M mide lo mismo que el ángulo:

a. O

b. P

c. Q

12. De acuerdo a la figura del problema 10, al lado OM le corresponde el lado:

a. OP

b. OQ

c. PQ

13. Si denominamos x a cada uno de los ángulos opuestos por el vértice O y z al ángulo marcado como 1 (ver figura del problema 10), se puede afirmar que el ángulo P (que es equivalente en medida al ángulo N) mide: Nota: recuerde que la suma de la medida de los ángulos internos de un triángulo da como resultado 180º.

a. 180-x+z

b. 180(-x+z)

c. x+z-180


14. Si PQ es es triple de MN, ¿qué se puede afirmar de la longitud del segmento OQ?

a. que es el triple de MN

b. que es el triple de ON

c. que es el triple de OM


15. En la figura 4 los dos triángulos comparten el ángulo de arriba, si el ángulo 1 y el ángulo 2 tienen la misma medida, se puede afirmar que:


a. El segmento de 180 metros es paralelo al de 300 metros.



b. El segmento de 180 metros es no es paralelo al de 300 metros.






16. Asumiendo que el ángulo 1 y el ángulo 2 tienen la misma medida (son congruentes), se concluye que los segmentos de 300 y 180 metros son paralelos, esto permitiría establer que:

a. 300 es a 180 como x es a 150, de donde se obtiene que x= 240

b. 300 es a 180 como x es a 150, de donde se obtiene que x=250

c. 300 / 180 = x /150, de donde se obtiene que x= 90

Responda los problemas del 17 al 20 de acuerdo con la siguiente información.

Dos ciudades A y B se encuentran sobre dos vias paralelas, como semumestra en el dibujo. Un cable de alta tensión abastece energía a la ciudad A desde la ciudad B, pasando por el peaje que se encuentra en el puente. El peaje y las dos ciudades son colineales (los tres puntos están sobre una línea recta, en este caso el cable que se ve desde arriba). Las dimensiones se muestran en la imagen.


17. Si la distancia del puente que le corresponde a la ciudad A se denomina con la incógnita X, la distancia del puente que le corresponde a la ciudad B tiene una longitud de:

a. x+500

b. x-500

c. 500+x

d. 500-x

18. Explique la razón por la cual los el ángulo de la ciudad A y el de la ciudad B son congruentes. Plantee la ecuación de suma interna de ángulos. Recuerde que en el peaje se forman ángulos opuestos por el vértice.

_____________________________________________________________

_____________________________________________________________

_____________________________________________________________

19. Para calcular la longitud L del cable de alta tensión es necesario resolver la ecuación:

a. 500²+250²=L

b. 500 + 250 = L²

c. 500²+250²= L³

d. 500² + 250² = L²

20. La longitud X que se menciona en el problema #17 se puede calcular resolviendo la ecuación:

a. 200/50 = (500+x)/x

b. 200/50 = (500-x)/x

21. La figura 5 muestra los triángulos RST y UVS, que son semejantes,ya que comparten el ángulo S, los ángulos RTS y UVS son congruentes y...

a. el ángulo R y el ángulo S son congruentes.

b. el ángulo R y el ángulo VUS son congruentes

c. el ángulo R y el ángulo SVU son semejantes.

22. De acuerdo con la figura 5, la longitud del segmento TS marcado con la incógnita es:

a. 22

b. 23

c. 24

d. 25

23. En el triángulo recto ABC, se ha trazado su altura desde el vértice B, que corta a AC en el punto D. Los lados del tríangulo miden 3, 4 y 5 cm. Se puede afirmar que los 5cm se deben a:

a. que si aplicamos el teorema de Pitágoras, se obtiene que AC equivale a la raíz cuadrada de la suma entre 4² y 3²

b. que si aplicamos el teorema de Pitágoras, se obtiene que AC equivale a la raíz cuadrada de la suma entre 5² y 3²

c. que si aplicamos el teorema de Pitágoras, se obtiene que AC equivale a la raíz cuadrada de la suma entre 4 y 3

24. Los triángulos rectos ABC y BDC, en la figura #6, son semejantes porque:

a. Comparten el ángulo B

b. Comparten el ángulo D

c. Comparten el ángulo C.

d. No son semejantes.

25. De acuerdo a la figura #6, la longitud del segmento AD adicionada con la longitud del secgemnto DC da como resultado:

a. 2

b. 3

c. 4

d. 5

26. En la figura #6 se deduce que AD + DC =5 y que si AD equivale a m, se obtiene que m+DC=5, donde DC equivale a:

a. m+5

b. m-5

c. 5-m

d. 5m

27. En la figura #6, los tríangulos BDC y ADC comparten el ángulo C y cómo son rectos, se concluye que:

a. Los triángulos son semejantes

b. Los triángulos son congruentes.

c. No es posible concluir congruencia.

d. Los triángulos son equivalentes.

28. En la figura #6, los tríangulos BDC y ADC son semejantes por compartir el ángulo C y ser rectos. Se puede establecer que la constante de proporcionalidad es:

a. 5

b. 5/3

c. 4/3

3/3

Taller de Estadística.

En construcción.........

COMASACA, Grado 9-1 y 9-2 Taller #1 de Recuperación de Matemáticas, Geometría y Estadística.

¿Por qué reforzar en matemáticas?

Cuando se enseña un saber matemático, es normal que no quede aprendido en su totalidad en el tiempo establecido, por esta razón se hace necesario buscar espacios y estrategias para reconceptualizar y retomar procesos matemáticos débilmente arraigados en nuestras estructuras de pensamiento. El propósito de este taller es el de hacer que tome mayor fuerza el aprendizaje adquirido, he allí la razón del término "reforzar" para este tipo de actividades escolares, que hacen parte de la didáctica de un conocimiento.

Algunos asuntos a manera de preliminares.

• Indicadores de desempeño.

Como es sabido desde el inicio del año escolar, los indicadores de desempeño para matemáticas en el primer periodo están relacionados con el insumo o tema de las funciones y en esencia la función lineal; en geometría lo relacionado a semejanza de triángulos y en estadística lo concerniente a técnicas de conteo y caracterización de variables.

• Presentación del documento final.

Es necesario dejar claro que el siguiente taller de refuerzo debe ser presentado en hojas cuadricula tamaño oficio o carta, con una hoja de presentación en la cual especifique la información necesaria para individualizar el documento. Además debe ir en primer lugar las correcciones de matemáticas, geometría y estadística. Pido que se copie la pregunta e inmediatamente la respuesta, no vaya a copiar todas las preguntas y luego responderlas porque no se revisa. Después de las correcciones de la evaluaciones, viene el desarrollo del taller de cada materia mencionada y finalmente las evaluaciones originales con la firma del acudiente. Recuerde que sin esta firma NO se revisa taller, además puede ser resuelto a lápiz, si desea puede copiar las preguntas a lapicero o recortarlas y pegarlas, a excepción de las gráficas o dibujos de geometría, los cuales deben ser construidos a mano.

Taller de Matemáticas.

Tema: Función y Función lineal.

1. Sea f una correspondencia de A en B definida como F={(x,y), x ϵ A ^ y ϵ B/ y = x(x+1)}, hallar las parejas que pertenecen a F si A={-1,0,1,2,3} y B={0,1,2,3,4,5}, luego indique por qué no es función.

2. Indicar cuales de las siguientes asignaciones son funciones de A en B con A={1,2,3}, y B={1,2,3} justificar la respuesta.

a. {(1,1),(2,1),(3,1)}
b.{(2,1),(3,2)}
c.{(1,1),(1,2),(2,3),(3,3)}

3. Escrbir el dominio y rango de la función g, con G={(2,4),(3,2),(1,0)}

4. Explique con un ejemplo por qué se afirma que una función es sobreyectiva cuando su codominio es equivalente al rango.

5. ¿Qué se puede decir de una función en la que se verifica que f(a)≠f(b) cuando a=b? Dar ejemplos.

6. ¿Qué se puede decir de una función en la que se verifica que f(a)=f(b) cuando a≠b? Dar ejemplos.

7. Sea X={1,2,3,4,5}, hallar el rango de la función f(x)=4x-5 de codominio Y={-5,-4,...,12,13,14,15}.

8. Represente gráficamente la función y=1-2x, mediante una tabulación con valores para x entre -5 y 5.

9. Despejar y en las siguientes ecuaciones:

a. x+y=5
b. x-y=5
c. 2x-3y=12
d. 3a+2b=6
e. 3(x-1) + 4(1-y)=0
f. x(x-1)+3y= x(x+1)+5y-100
g. 1/x +y=3
h. x=1/(y-1)

10. Indique cuáles de las ecuaciones del problema, representan líneas rectas. Aplique el flujograma visto en clase para clasificar funciones lineales.

11. Represente en el plano cartesiano algunas parejas (x,y) tales que la suma de las abscisas con las ordenadas sea cero.

12. Represente en el plano cartesiano algunas parejas (x,y) tales que la diferencia entre las abscisas con las ordenadas sea cero.

13. Represente en el plano lasparejas (x,y) tales que x por y sea equivalente a 12. (algebraicamente xy=12) ¿Qué concluyes del lugar geométrico de puntos obtenidos? ¿Es una línea recta en el plano? Explica.

14. Una persona recorre 4 km en 10 minutos, es de esperarse que el doble de esta distancia la haga en 20 minutos y que el triple la haga en 30 minutos. Represente esta situación el plano cartesiano donde la distancia esté en función del tiempo.

15. Una persona recorre 4 km en 10 minutos, pero el doble de esta distancia no la hace en 20 sino en 15 minutos. ¿En cuánto tiempo recorrerá 12 km? Graficar, hallar la pendiente de la recta, reemplazar en la ecuación punto pendiente y escribir la ecuación que relaciona la distancia x con el tiempo t que tarda en recorrerla.

16. Hallar la pendiente de la recta que pasa por los puntos (2,3) y (5,-4)

17. Por cada 20 cm de altura de una rampa, se avanzan 30 cm. ¿Qué altura h tiene una rampa en la cual se han avanzado 200 metros al final? Plantear ecuación y resolverla para h.

18. Una empresa de celulares calcula que el pago P (en pesos) de un usuario que consume t minutos está dado por a ecuación p=500(200+t):

a. ¿Cuánto le cobran por t=0 minutos? ¿Este valor qué representa en la recta?
b. ¿Calcule la pendiente entre t=20 minutos y t= 30 minutos. ¿Qué representa este valor en la recta y en el contexto del problema?
c. Calcular t para un consumo p=$14.000
d. Represente p en función de t.

19. Dos rectas en el plano son paralelas si tienen pendientes equivalentes. Indique cuáles de las siguientes ecuaciones de recta, al representarlas en el plano, son paralelas a 2x-3y= 15

a. y=2x-3
b. y=0.5x-4
c. y=4/6 x-1
d. y=3/2 x+4

20. Dos vehículos parten de manera simultánea y en sentidos opuestos, desde dos ciudades distantes 50 km y en línea recta. El primero rcorre una distancia x en km en un tiempo t en horas, de acuerdo a la ecuación x=4t+2 y el segundo de acuerdo a la ecuación x=2t+6.
a. ¿Cuánto tiempo tardan los vehículos en llegar a la ciudad opuesta?
b.¿Cuál de los dos llega primero?
c. Cuando llega el primer vehículo a su ciudad opuesta, ¿cuánto le falta al otro para llegar?
d. En el viaje, ¿en que momento (timpo) se encuentran?
e. Represente los dos movimientos en el plano de tal manera que x esté en función de t, ¿qué concluyes?


Taller de Geometría.


Taller de Estadística.

En construcción.........